Fixed Axis Rotation in Rigid Bodies Using Vectors
This section presents relative motion using vector notation.
When moving from particle kinematics to rigid body kinematics, we add the rotation of a body into the motion analysis process. Some bodies will translate and rotate at the same time, but many engineered systems have components that simply rotate about some fixed axis. We will start our examination of rigid body kinematics by examining these fixed axis rotation problems, where rotation is the only motion we need to worry about.

|
|
Angular Position, Velocity, and Acceleration.
Just as with translational motion, we will have angular positions, which we can take the derivative of to find angular velocities, which we can again take the derivative of to find angular accelerations. Since we can only have a single axis of rotation in two dimensional problems (rotating about the z axis, with counter-clockwise rotations being positive, and clockwise rotations being negative) the equations will mirror the one dimensional equations used in particle kinematics.
| Angular Position: | \[\theta(t)\] |
|---|---|
| Angular Velocity: | \[\omega(t)=\frac{d\theta}{dt}=\dot{\theta}\] |
| Angular Acceleration: | \[\alpha(t)=\frac{d\omega}{dt}=\frac{d^2\theta}{dt^2}=\ddot{\theta}\] |
Also as with one dimensional translational motion, we can use integration to move in the opposite direction (just remember your constants of integration).
| Acceleration: | \[\alpha(t)\] |
|---|---|
| Velocity: | \[\omega(t)=\int \alpha(t)\] |
| Position: | \[\theta(t)=\int \omega(t)=\iint \alpha(t)\] |
If we have constant angular accelerations, we can also use the following formulas adapted from one dimensional motion.
| Acceleration: | \[\alpha(t)=\alpha\] |
|---|---|
| Velocity: | \[\omega(t)=\alpha t+\omega_{0}\] |
| Position: | \[\theta(t)=\frac{1}{2}\alpha t^{2}+\omega_{0}t+\theta_{0}\] |
| Without Time: | \[\omega^{2}-\omega{_{0}}^{2}=2\alpha(\theta-\theta_{0})\] |
Velocity and Acceleration of a Point on a Rotating Body:
With fixed axis rotation, there is a single point on a body that does not move, however all other points on this body will have some velocity and some acceleration due to the rotation of the body itself.
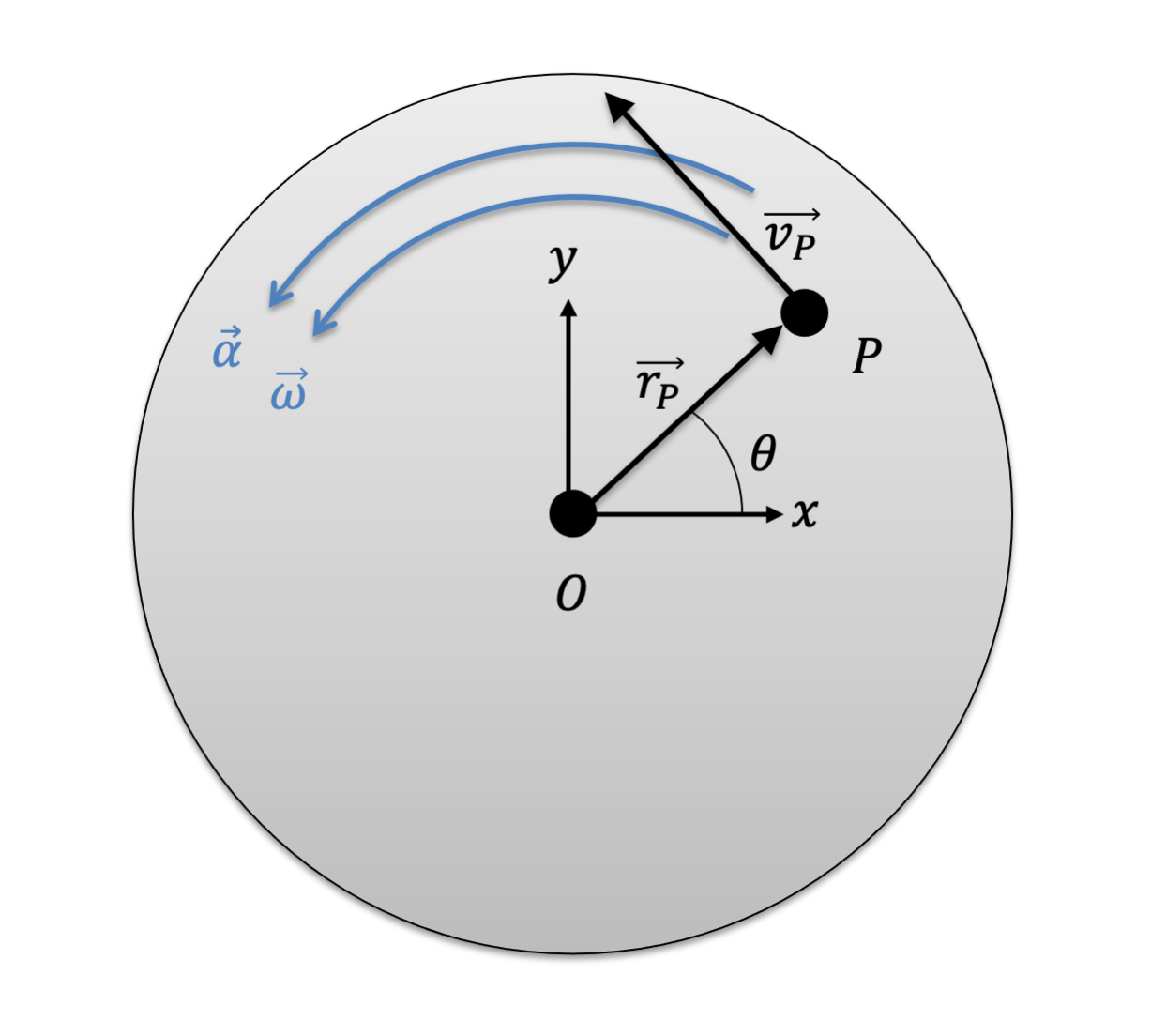
To determine the velocities and accelerations of these points, we will derive vector equations in rectangular coordinates. First, we decompose the position vector rP into x and y components.
| Position of P with respect to the fixed axis: | \[ \vec{r_P} = r_P cos\theta \hat{i} + r_P sin \theta \hat{j} \] |
|---|
We will then take the derivative of rP with respect to time, using the product rule. This will give us the velocity of P.
| \[ \vec{v_P} = \frac{d}{dt}(r_P) cos\theta \hat{i} + r_P \frac{d}{dt}(cos\theta) \hat{i} + \frac{d}{dt}(r_P) sin \theta \hat{j} + r_P \frac{d}{dt}(sin \theta) \hat{j}\] |
To simplify the above equations, we can note that for a rigid body, the point P never gets any closer or further away from the fixed center point O. This means that the distance rP never changes and the derivatives of rP in the above equations are zero. Putting this to work, we can simplify the above equation into the equation below.
| \[ \vec{v_P} = r_P \frac{d}{dt}(cos\theta) \hat{i} + r_P \frac{d}{dt}(sin \theta) \hat{j}\] |
| \[ \vec{v_P} = r_P (-sin \theta) \dot{\theta} \hat{i} + r_P (cos\theta) \dot{\theta} \hat{j}\] |
Rearranging the equation, we can find the final expression we will use.
| \[ \vec{v_P} = \dot{\theta} \hat{k} \times (r_P cos\theta \hat{i} + r_P sin \theta \hat{j}) \] |
| \[ \mathbf{\vec{v_P} = \vec{\omega} \times \vec{r_P}} \] |
In a similar way, we can find an expression for the acceleration of point P.
| \[ \vec{a_P} = \vec{\alpha} \times \vec{r_P} + \vec{\omega} \times (\vec{\omega} \times \vec{r_P})\] |
For planar motion, the vectors omega and rP will always be perpendicular to each other, so we can simplify further.
| \[ \mathbf{\vec{a_P} = \vec{\alpha} \times \vec{r_P} - \omega^2 \vec{r_P}}\] |
The acceleration of point P has two components. Note that the omega-squared in the second term is not a vector - it's the scalar value of omega. The direction of that term is defined by the vector rP. In planar motion, the two components are perpendicular to each other. We can describe them as occurring in the normal and tangential directions.
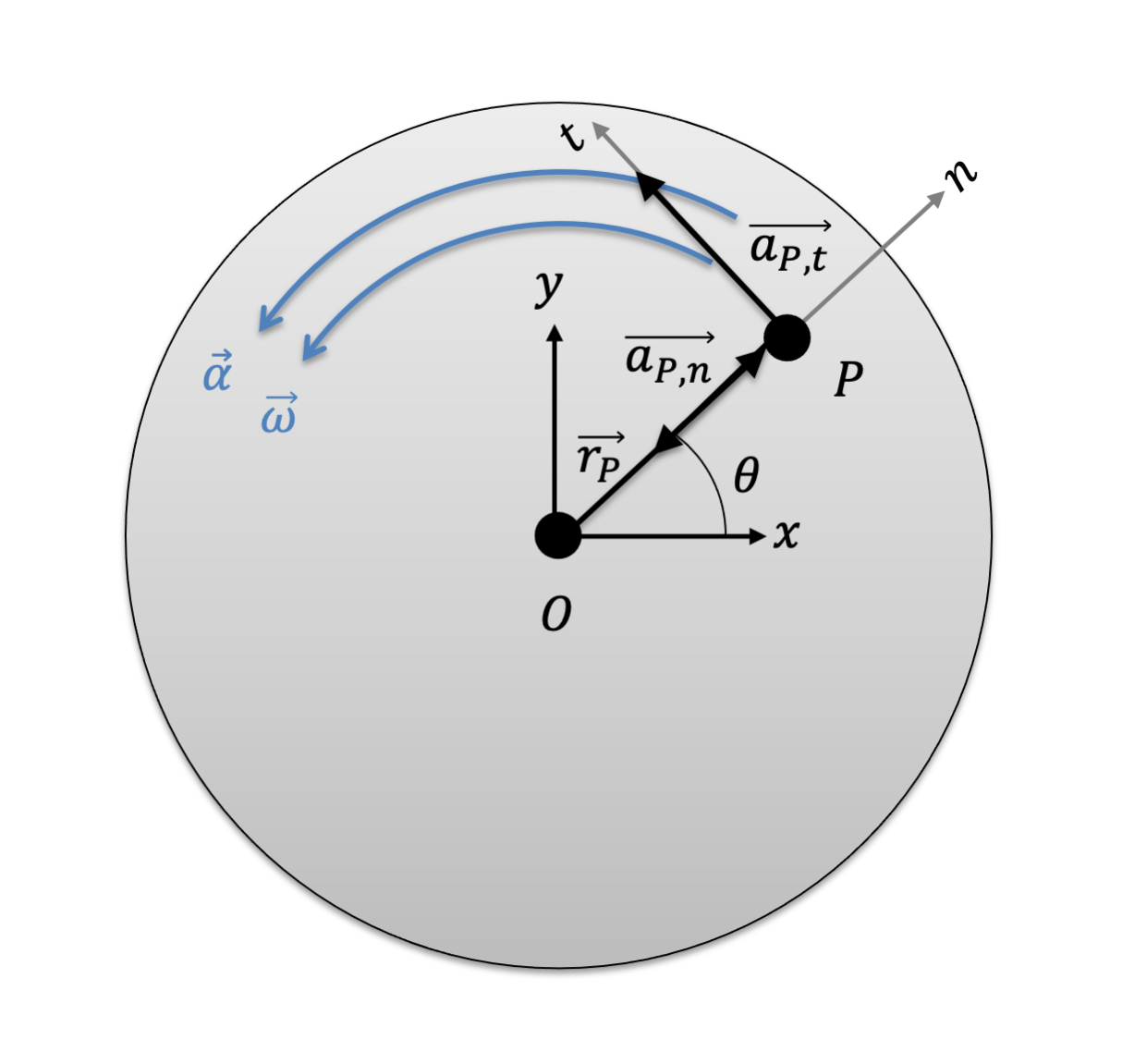
| \[ \vec{a}_{P,t} = \vec{\alpha} \times \vec{r}_{P} \] |
| \[ \vec{a}_{P,n} = - \omega^2 \vec{r}_{P}\] |
These equations allow us to find the velocity and acceleration of any point on a body rotating about a fixed axis, given the vectors for angular velocity of the body (omega), the angular acceleration of the body (alpha), and the position of the point with respect to the axis of rotation (rP, or alternately written as rP/O).