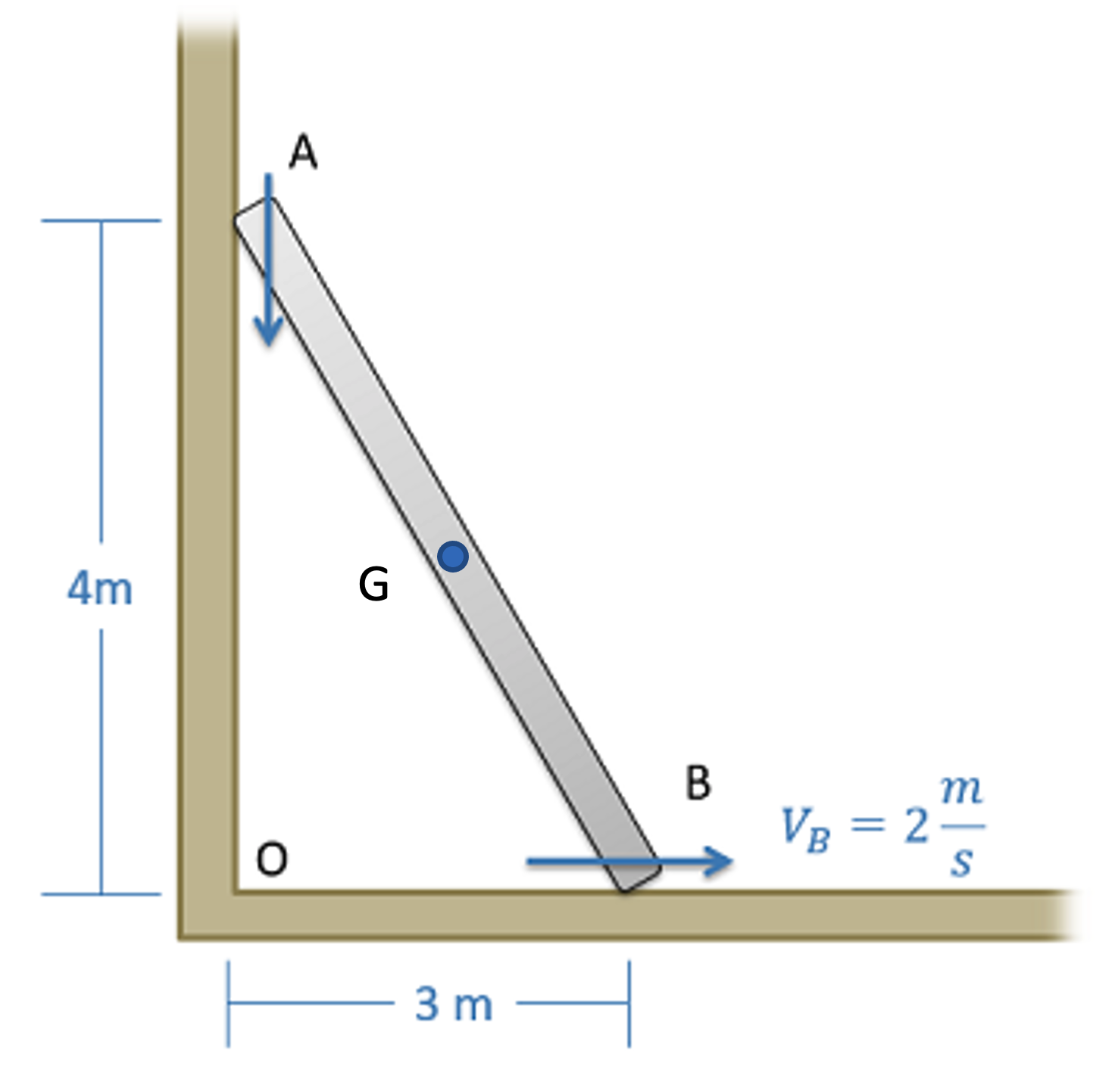
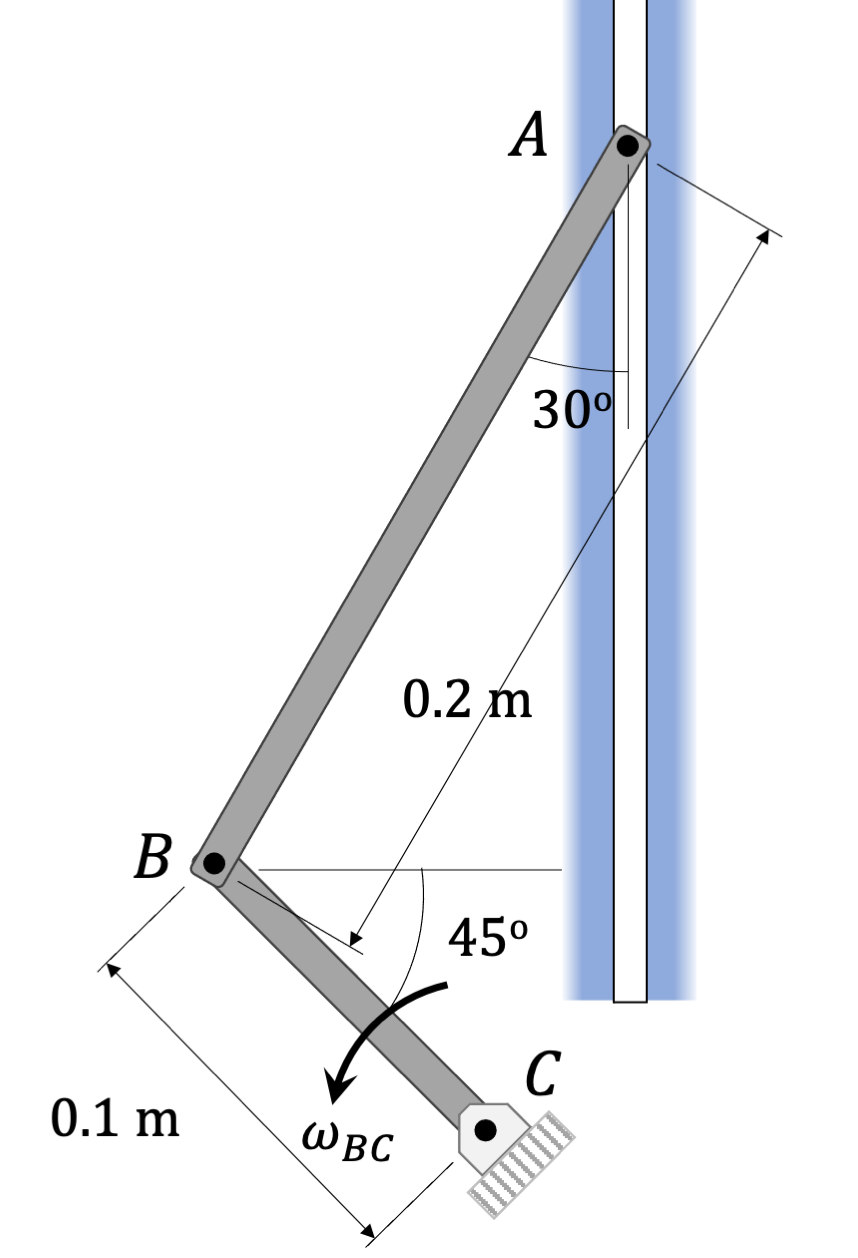
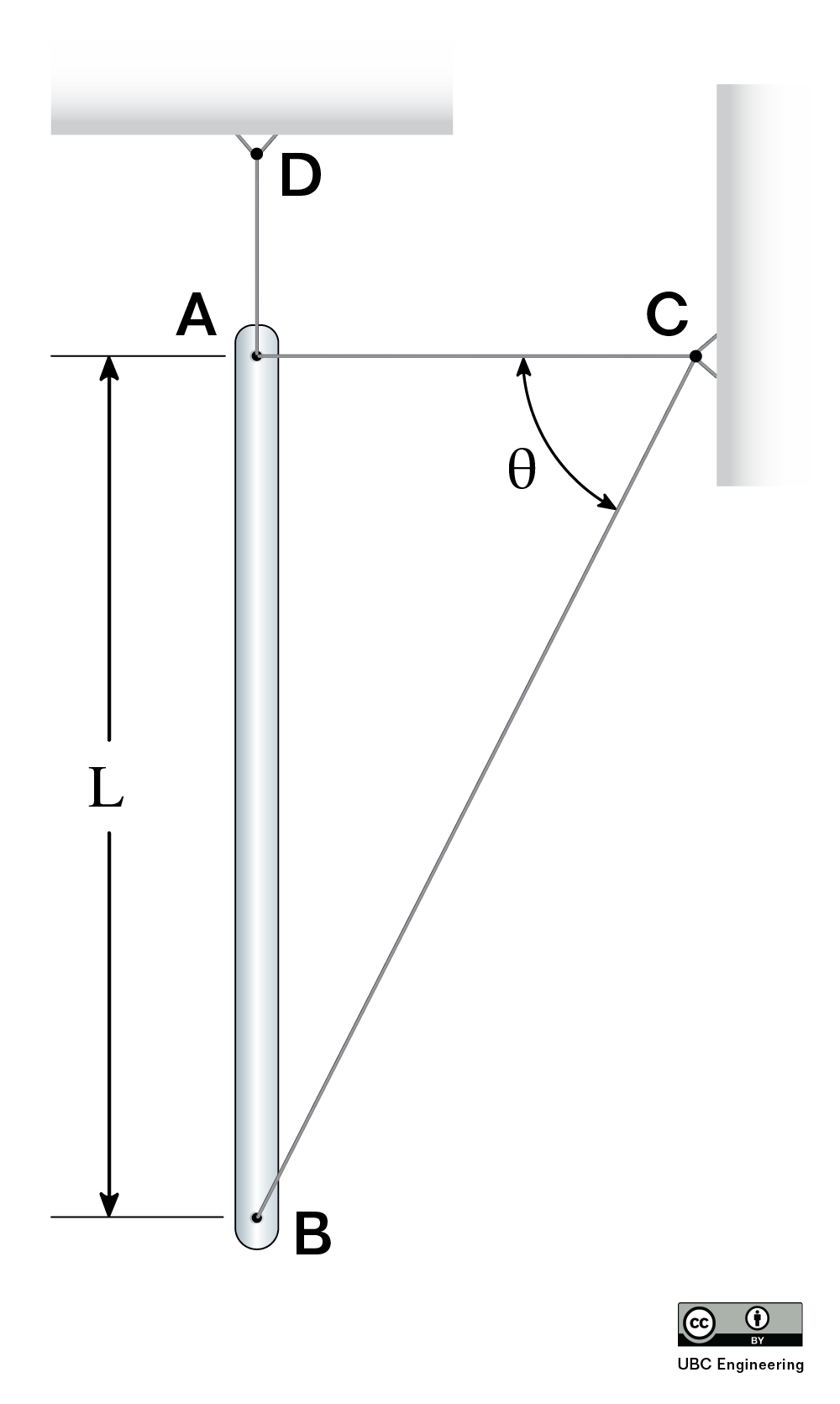
Instantaneous Center of Zero Velocity (ICZV)
This section presents relative motion using vector notation.
Instantaneous Center of Zero Velocity is a graphical technique that can help simplify relative motion problems. At any instant in time, a rigid body undergoing general planar motion may appear to be rotating around a particular point. Finding this point allows you to use simpler equations for fixed rotation to analyze the motion of that body. In some cases, this simplifies the solution.
Finding the Instantaneous Center of Zero Velocity (ICZV)
To find the ICZV (also denoted "IC") for a rigid body, you need to know the direction (but not the magnitude or the sense) at two points on the same rigid body. If the velocities at the two points are parallel, then you need additional information. We will start with the simpler case of non-parallel velocities at two points.
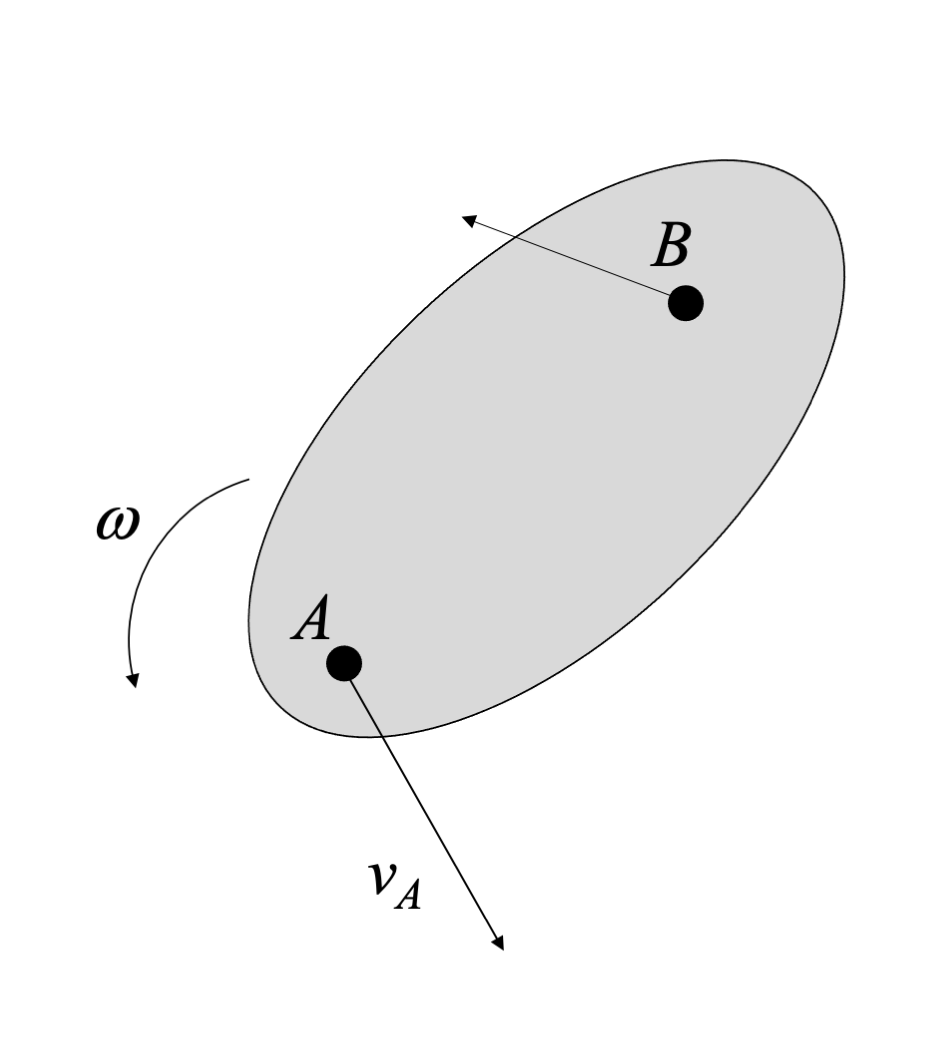
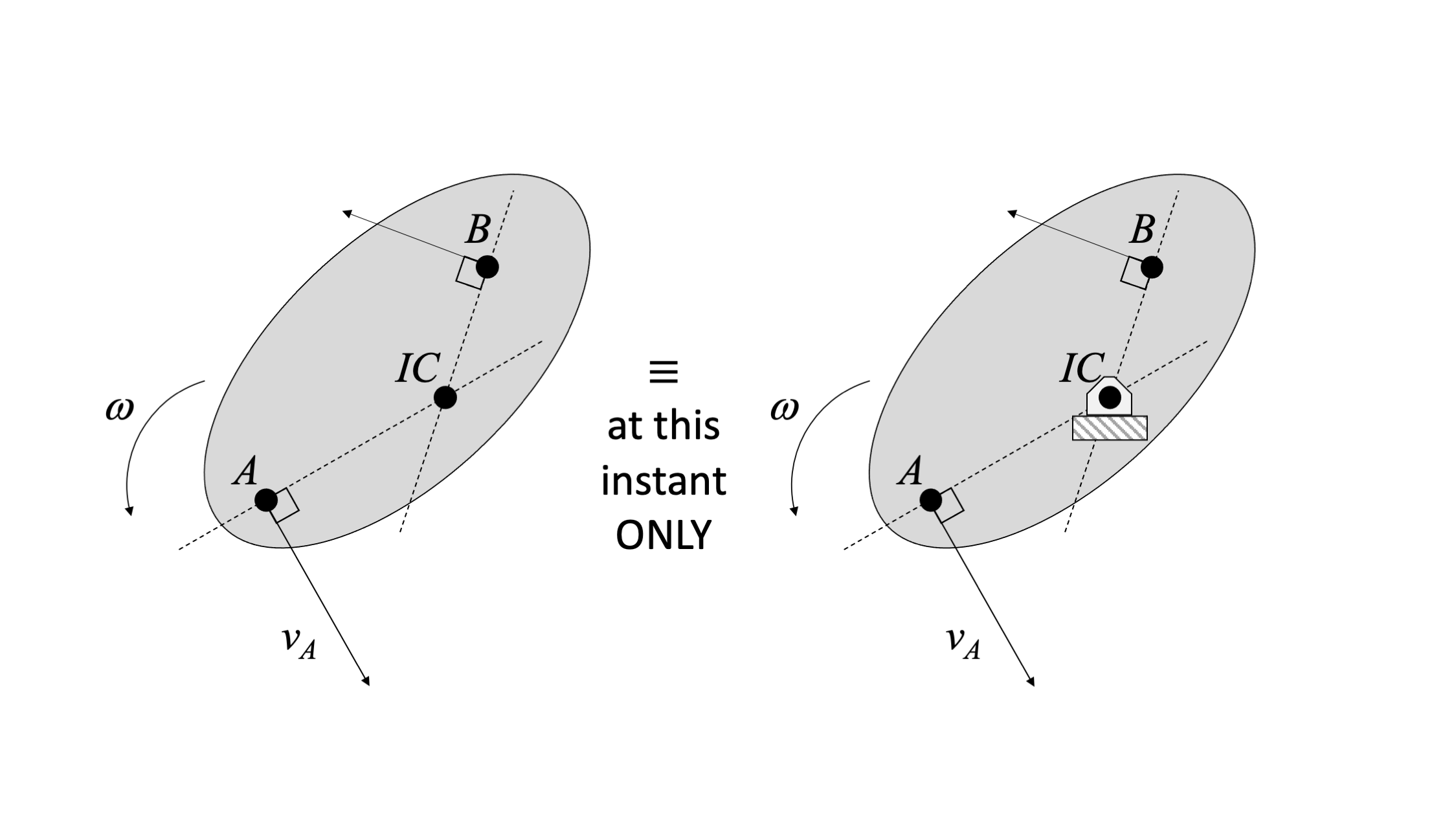
Once you have identified two non-parallel point velocities, draw lines perpendicular to those velocity directions. The point where the perpendiculars meet is the ICZV. At this point, the velocity of the body is zero. Note that the IC can be on or off the body. If the IC is off the body, you can imaging massless rods connecting the IC to the rigid body.
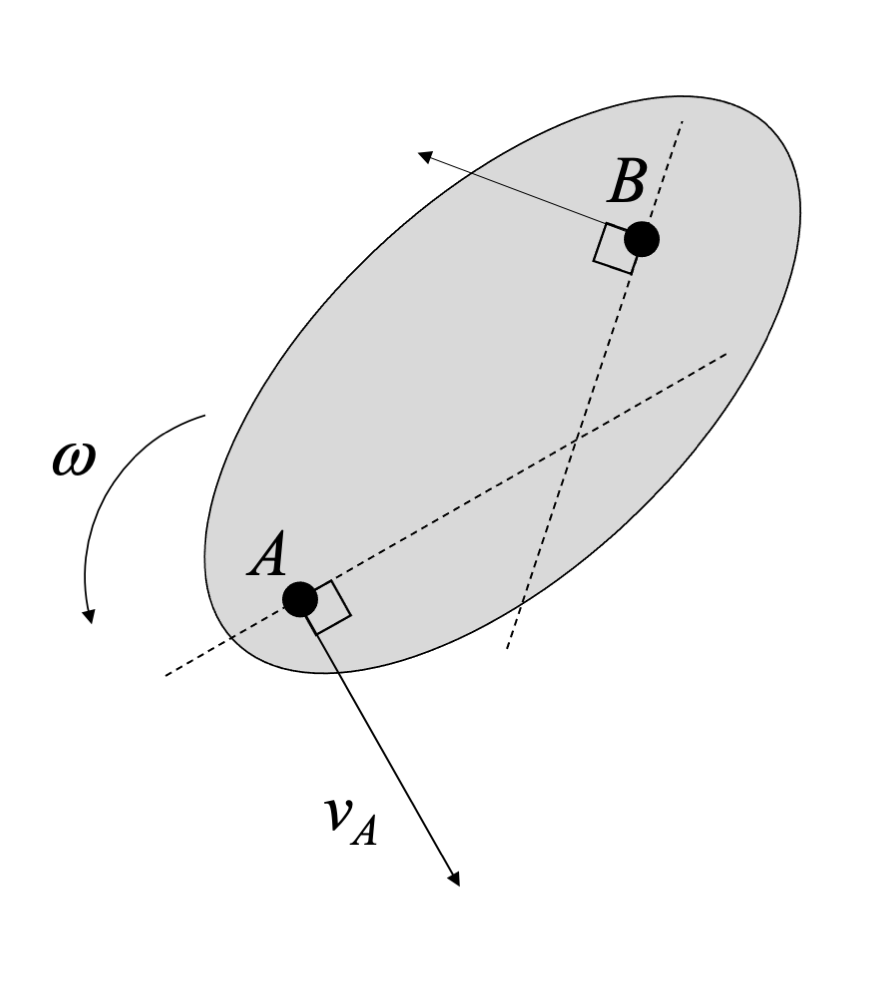
If this was actually pure rotation, with a physical pin at the location of the IC, we'd expect all points on the body would have velocities perpendicular to the position vector between the pin and the point of interest. The IC gives us the same effect.
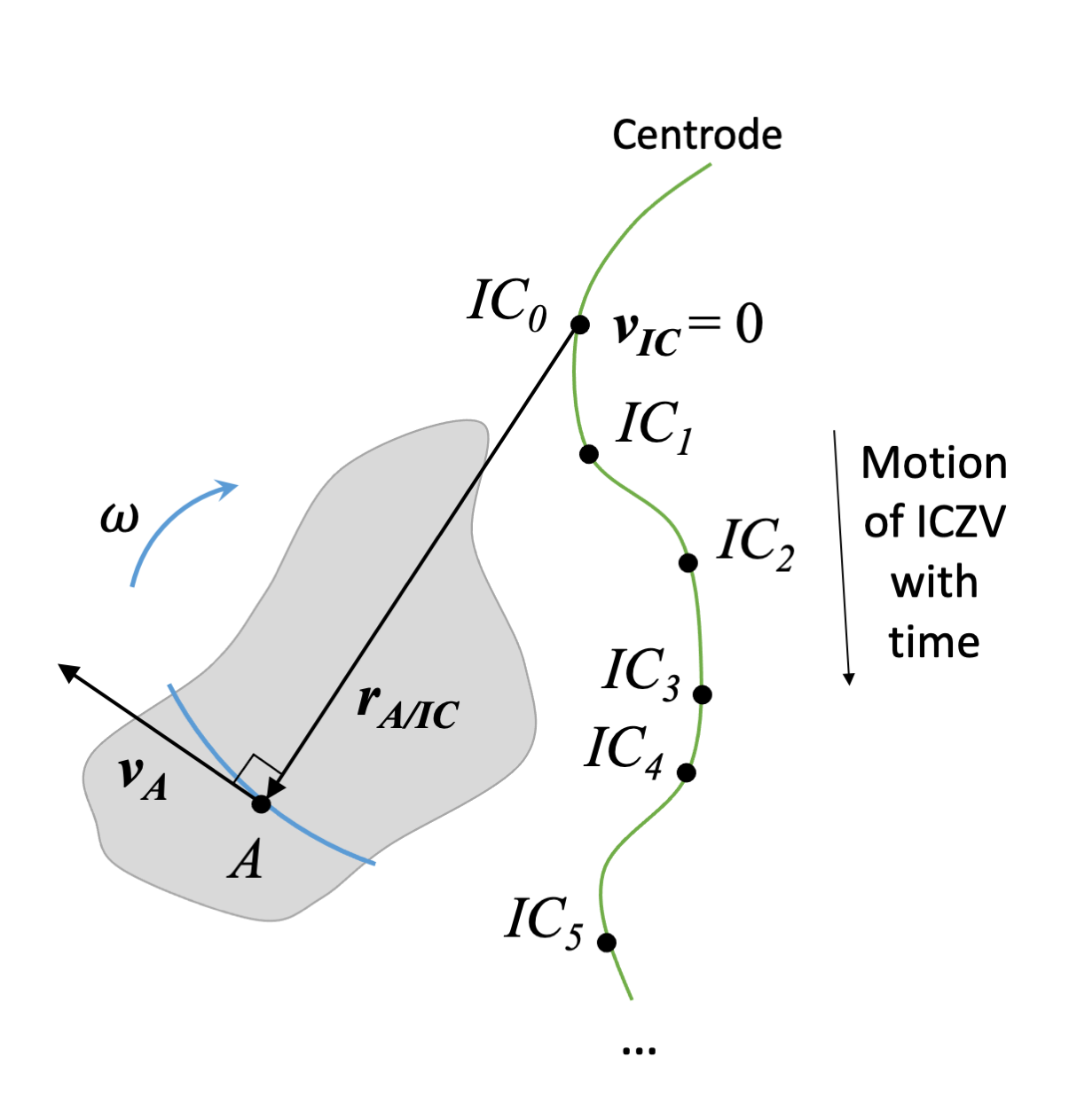
However, unlike a physical pin, in the next instant the ICZV location can change. The path of the ICZV is called a centrode.
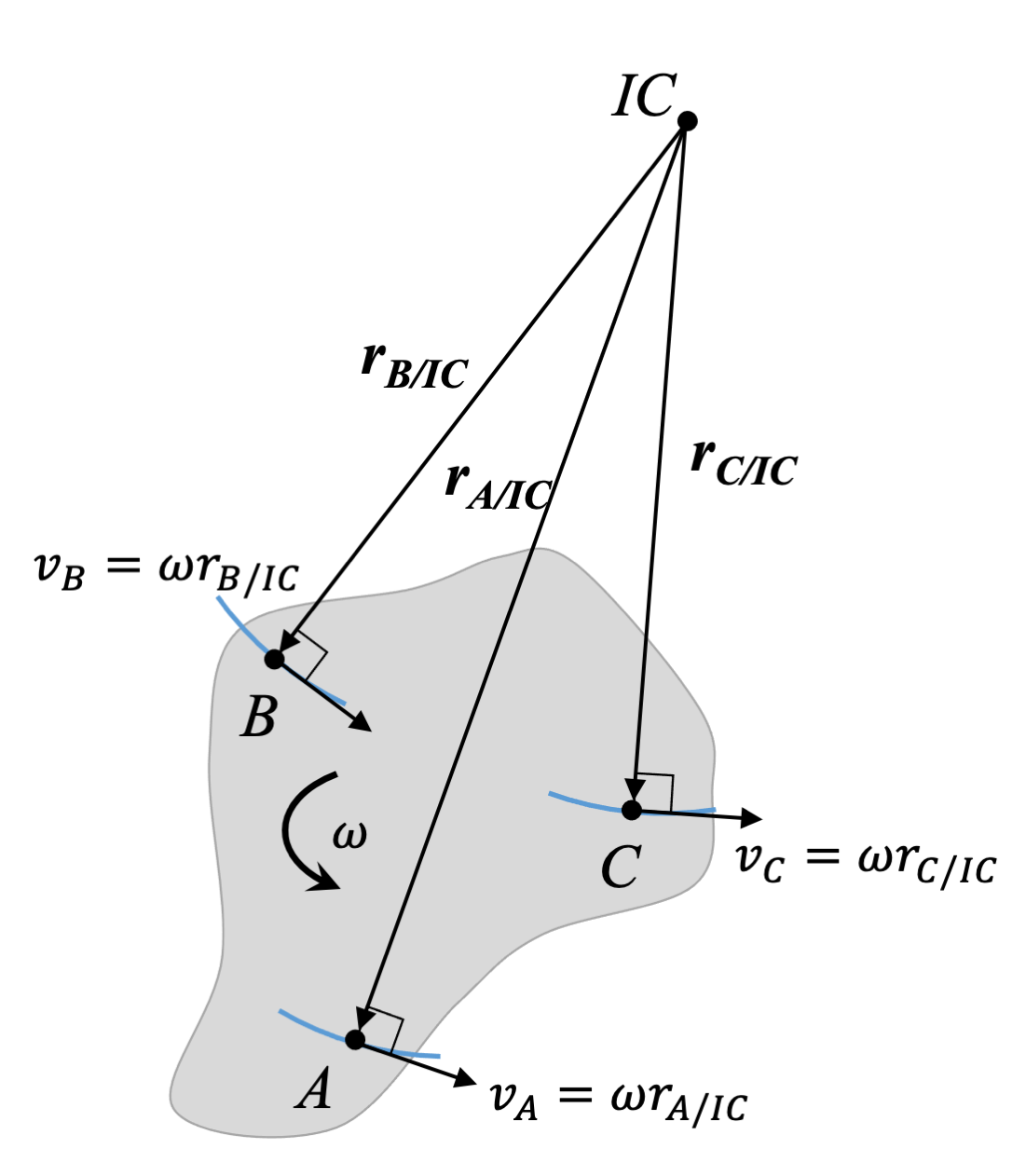
Since many rigid body kinematics problems involve finding a velocity at a particular instant, the ICZV can be a useful tool. In many cases, it is used to quickly find the velocity at a third point on a body undergoing general plane motion. This can be done using the fixed axis rotation velocity equation:
| Velocity using ICZV: | \[\vec{v}_{C}=\vec{\omega} \times \vec{r}_{C/IC}\] |
|---|
Finding ICs when velocities are parallel
When the two velocities are parallel, we need some additional information about sense and/or magnitude, and we find the IC in a slightly different way.
To find the IC when velocities are parallel, draw a line that connects the two vector heads, and another line that connects the two vector tails.
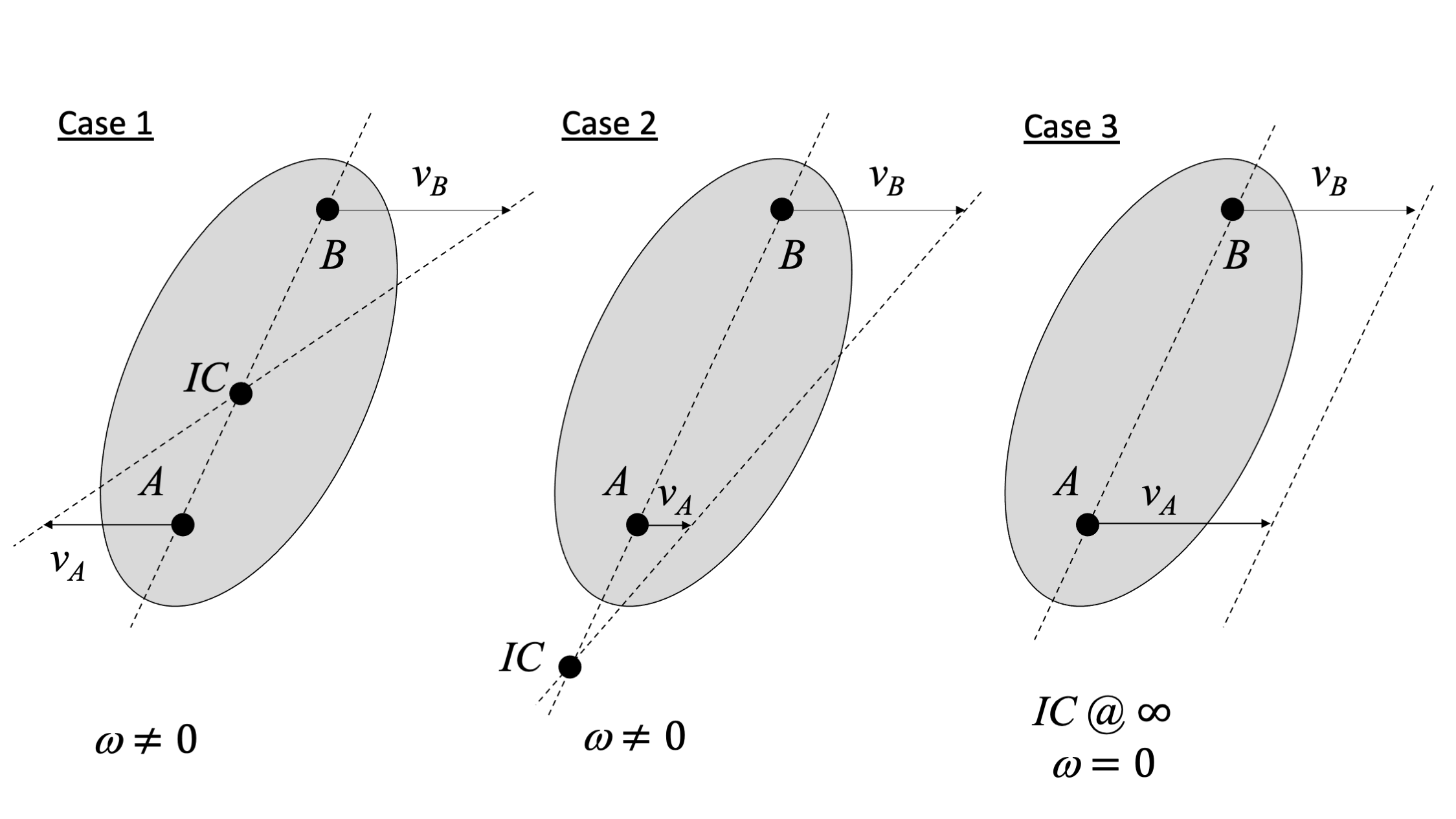
Case 1: Opposite senses
When the two velocities are parallel but have opposite senses (e.g. one is directed toward positive x and the other toward negative x), the object is rotating and you will find an IC. The IC will be located on the line between the two points. The location of the IC will depend on the magnitudes of the vectors.
Case 2: Same sense, different magnitude
When the vectors have the same sense (e.g. both directed toward positive x), then you also need magnitude to know if an IC exists. If the magnitudes are different, the object is rotating. The IC will be located on the line passing through both points, past the point with lower velocity.
Case 3: Same sense, same magnitude
If two points on a rigid body have the same velocity vector, then the body is not rotating. If we draw the lines connecting the two heads and the two tails, we will get parallel lines. The intersection of parallel lines is at infinity. There is no useful IC in this case.
There are a few important things to remember when using the ICZV:
- The ICZV is only a model - there is no actual pin.
- The ICZV typically changes location over time. An ICZV is only useful at this instant.
- The ICZV is for velocity only. The ICZV will not necessarily have zero acceleration.