Position, Displacement, Velocity, and Acceleration
After discussing bodies, the next important concepts in engineering mechanics are the concepts of position, displacement, velocity, and acceleration. Collectively these concepts will define the motion of the body over time. Though you may have heard of these concepts before, it is important to fully define them, as they have specific and precise meanings in engineering mechanics.
Position
The position of a body is simply the current location of that body. For particles, this will be easy to identify, but for extended bodies (which we often call rigid bodies) it is a little more complicated. This is because the position could refer to the location of any point on the body. In engineering mechanics though, unless otherwise specified, the position of a rigid body usually refers to the location of the center of mass of that body.
We have two options for quantifying the position of a body. We can either specify a distance and direction from some set origin point or we can give the location based on distances from the origin in the set coordinate directions. In either case it will first be important to identify an origin point where we will be measuring from and to identify the coordinate axes we will be using. Without this information we cannot fully define the position, and it is therefore essential that we clearly identify these in the problems we are working with.
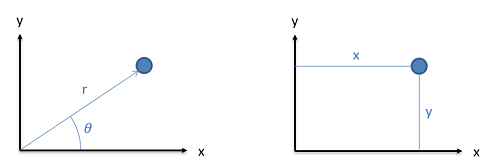
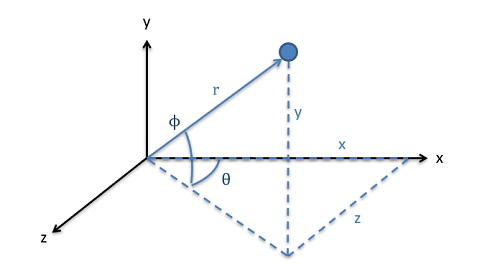
If we move to a three dimensional system, we will still have two options for defining position, but we will now need two angles and a distance or we will need distances in three coordinate positions.
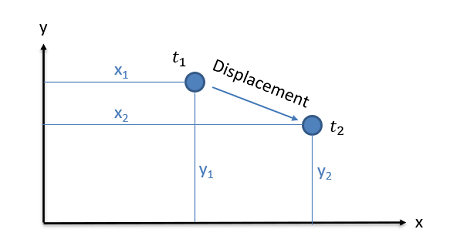
Displacement
The displacement of a body is simply the change in position between two points in time. Displacement is a vector quantity, where we will need to know not only how far the object has moved, but what direction it has moved in.
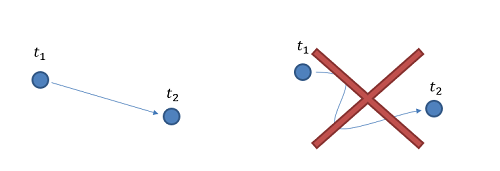
Another important aspect of displacement is that it is path independent. Regardless of the path taken between time one and time two, the displacement is the direct route between those positions.
Velocity
The velocity of a body is defined as the rate of change of the position of the body divided by the rate of change of time at any given instant.
| \[\vec{v}=\frac{d\vec{r}}{dt}\] |
Again this is a vector quantity, having both a magnitude and a direction. If we want to talk about just the magnitude of the velocity vector, that is the speed.
If we are interested in the average velocity over some set time period, we would take the change in position (which is the displacement) over the change in time.
| \[\vec{v}_{ave}=\frac{\Delta \vec{r}}{\Delta t}=\frac{displacement}{time}\] |
Acceleration
Finally, the acceleration is defined as the rate of change of velocity over the rate of change of time. Since velocity itself is the rate of change of position over time, the acceleration is then the double derivative of the position with respect to time.
| \[\vec{a}=\frac{d\vec{v}}{dt}=\frac{d^2\vec{r}}{dt^2}\] |
As with displacement and velocity, acceleration is a vector quantity with both a magnitude and direction. Acceleration will exist whenever there is a change in velocity, whether that is a change in speed or a change in direction.