Varignon's Theorem

Varignon's Theorem, also often called the principle of moments, is a very useful tool in scalar moment calculations. In cases where the perpendicular distance is hard to determine, Varignon's Theorem offers an alternative to finding that distance.

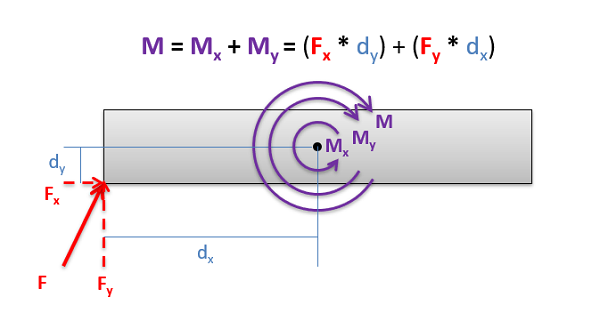
In it's basic form, Varignon's states that if we have two or more concurrent forces, the sum of the moments that each force creates about a single point will be equal to the moment created by the sum of those forces about the same point.

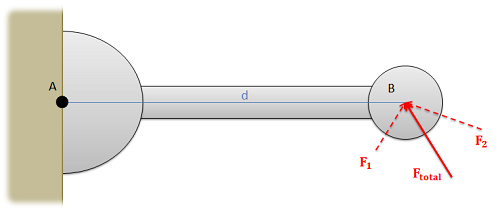
Two concurrent forces acting on a lever arm
If the sum of F1 and F2 is Ftotal, then we can assume that the sum of the moments about point A exerted by F1 and F2 will be equal to the moment exerted about point A by Ftotal

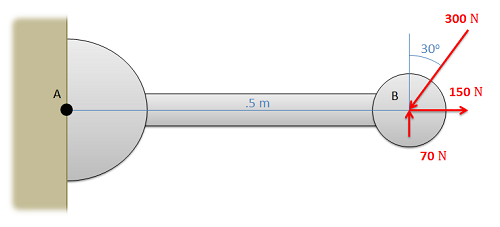
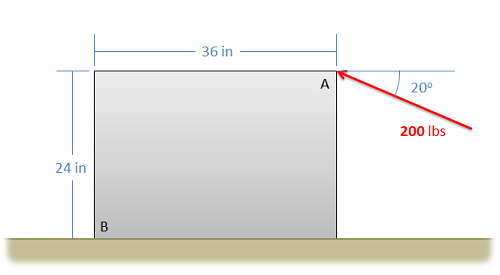
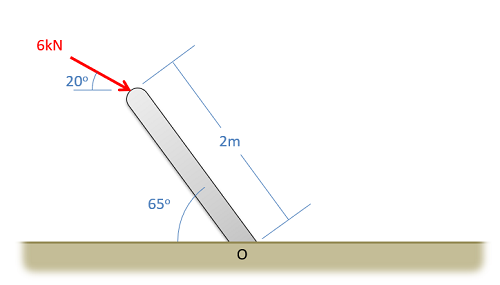
On it's surface this doesn't seem that useful, but in practice we will often use this Theorem in reverse by breaking down a force into components (the components being a set of concurrent forces). We can solve for the moment exerted by each component (where perpendicular distance d is easier to find) and then simply add together the moments from each component to find the moment from the original force.

Breaking a force into components to solve for the overall moment
When finding the moment of Force F about the center point, it will be easier to break down the force into components and find the moments of each component rather than trying to find the perpendicular distance directly using complex geometric relationships.

Worked Problems:

Question 1:

Use Varignon's Theorem to find the moment that the forces in the diagram below exert about point A.

Problem 1 Diagram

Solution:



PDF Solution

Question 2:

Use Varignon's Theorem to determine the moment that the force at point A exerts about point B.

Problem 2 Diagram

Solution:



PDF Solution

Question 3:

Use Varignon's Theorem to determine the moment that the force shown below exerts about the base of the post at point O.

Problem 2 Diagram

Solution:



PDF Solution