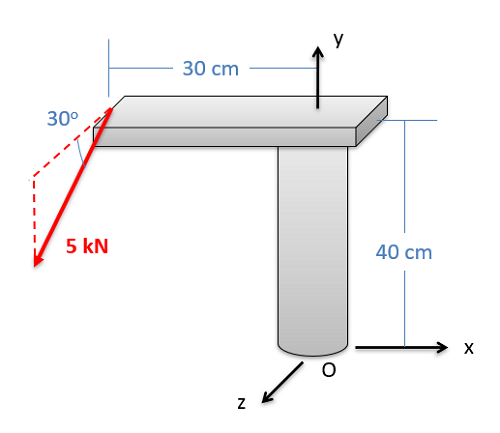
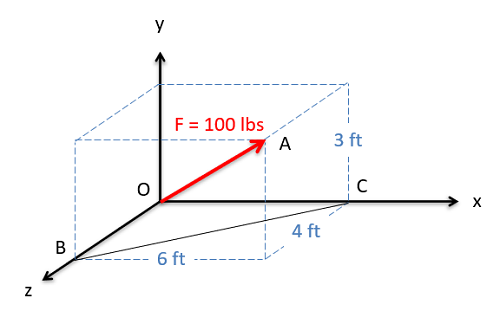
Moment of a Force About an Axis

It is sometimes useful to be able to calculate the moment a force exerts about a certain axis that is relevant to the problem. An example would be a force on the vault door in the image to the right. If we took the moment about a point (say one of the hinges on the door) we may find that the moment vector does not line up with the axis of this hinge. In that case, the component of the moment vector that lines up with the axis of the hinge will cause a rotation, while the component of the moment vector that does not line up with the axis of the hinge will cause reaction moments in the hinge. If we are only interested in the rotation of the door, we will want to find the moment that the force exerts specifically about the axis of the hinges.
Calculating the Moment About an Axis via the Dot Product:
To find the moment of a force about a specific axis, we find the moment that the force exerts about some point on that axis and then we find the component of the moment vector that lines up with the axis we are interested in.
To do this mathematically, we use the cross product to calculate the moment of the force about any point along the axis, and then we take the dot product of a unit vector along the axis and the moment vector we just calculated.
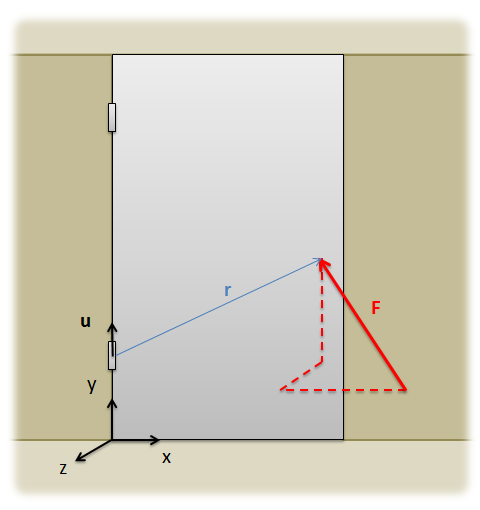
| \[M=\vec{u}\cdot \left ( \vec{r}\;\times \vec{F} \right )\] |
The unit vector u has a magnitude of one and will be pointing in the direction of the axis we are interested in. Your final answer from this operation will be a scalar value (having a magnitude but no direction). This is the magnitude of the moment about the given axis, with the direction being specified by the unit vector u.