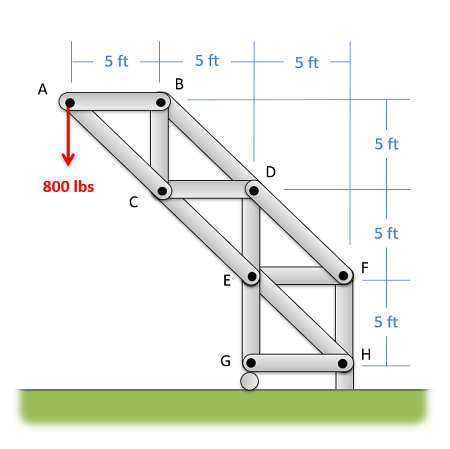
The Method of Sections
The method of sections is a process used to solve for the unknown forces acting on members of a truss. The method involves cutting the truss into individual sections and analyzing each section as a separate rigid body. Where the method of joints is the fastest way to find the forces in all members, the method of sections is usually the fastest and easiest way to determine the unknown forces acting in a specific member of the truss.
Using the Method of Sections:
The method of sections and the method of joints both have the same initial steps, but will differ from one another once the external forces are found. The process used in the method of sections is outlined below.
To start, if the joints are not already labeled, we will begin by labeling all the joints with a letter. The exact order you label the joints in are not important, so long as you are consistent in your work. We will refer to joints by their letter (A, B, C...) and we will refer to the members by the two joints they connect (AB, AC, BC...). As a note, this text will always arrange the member names alphabetically, in order to avoid confusion (member AB, rather than member BA)
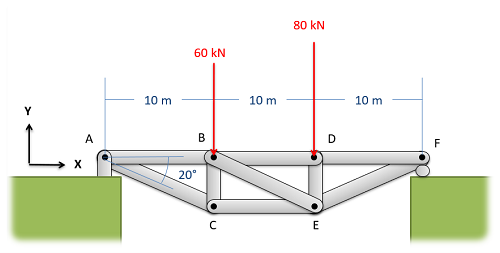
The second step is to solve for the external reaction forces supporting the truss. We can sometimes skip this step if the reaction forces are not necessary to solve for the internal forces, but when in doubt it is better to solve for the external reaction forces up front. To do this, treat the whole truss as a single rigid body. Draw a free body diagram of the truss, including the load forces and the external reaction forces supporting the truss, write out your equilibrium equations (sum of forces in the x, sum of forces in the y, and sum of moments), and finally solve the equilibrium equations for the unknown reaction forces.
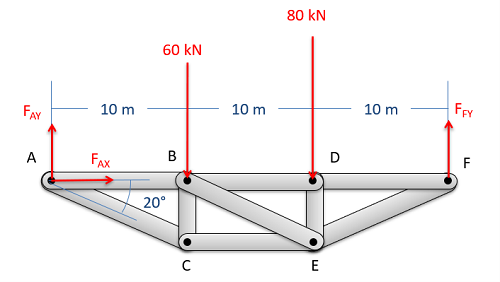
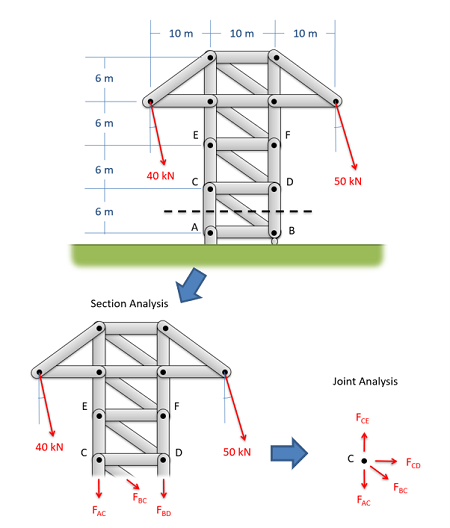
Next, to get to the heart of the method of sections, you will imagine cutting your truss into two separate sections. This cut should only travel through members (don't cut at a joint) and should cut through the member (or members) that you are trying to solve for. We should also try and minimize the number of members we cut though, limiting ourselves to a maximum of three members for a two dimensional problem.
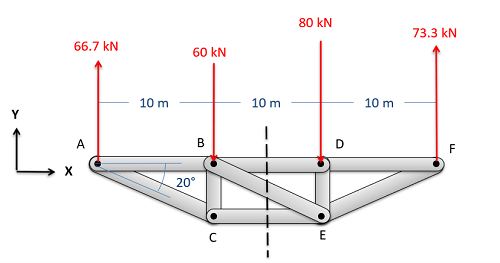
After determining the cut you want to use, you will next draw a free body diagram of one half of the truss. This can be the half on either side of the cut you define, though choosing the side with fewer external reaction forces acting on it will generally make analysis easier. When drawing the free body diagram of this section be sure to include and label all known and unknown forces the forces acting on that section.
The known forces will be all load forces and external reaction forces acting on the half of the truss we are analyzing. Load or reaction forces acting on the other half of the truss should not be included on the free body diagram.
The unknown forces in the free body diagram should be the forces carried by the members that we cut through. As the members are all two force members, we will draw in one single tensile force for each member we cut through. This force will act along the line of the member itself. Just as with the method of joints, we do not know if the members are in tension or compression. However, if we assume tension then positive answers indicate the member is actually in tension while negative numbers indicate the member is in compression.
In the free body diagram, make sure you label all forces, and indicate important angles and dimensions.
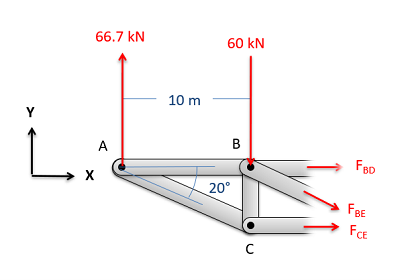
Next you will want to write out the equilibrium equations for the section you just drew. These will be rigid bodies, so you will need to write out the force and the moment equations.
For 2D problems you will have three possible equations for each section, two force equations and one moment equation.
| \[\sum F_x=0\] | \[\sum F_y=0\] | \[\sum M_z=0\] |
For 3D problems you will have six possible equations for each section, three force equations and three moment equations.
| \[\sum F_x=0\] | \[\sum F_y=0\] | \[\sum F_z=0\] |
| \[\sum M_x=0\] | \[\sum M_y=0\] | \[\sum M_z=0\] |
Finally, solve the equilibrium equations for the unknowns. You can do this algebraically, solving for one variable at a time, or you can use an equation solver to solve for everything at once. If you assumed that all forces were tensile earlier, remember that negative answers indicate compressive forces in the members.
Extending the Method of Sections:
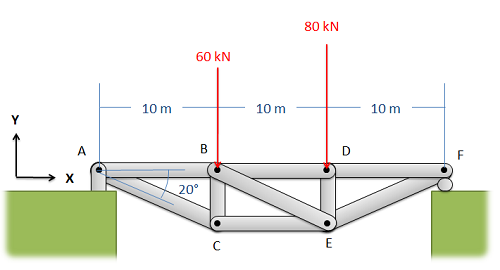
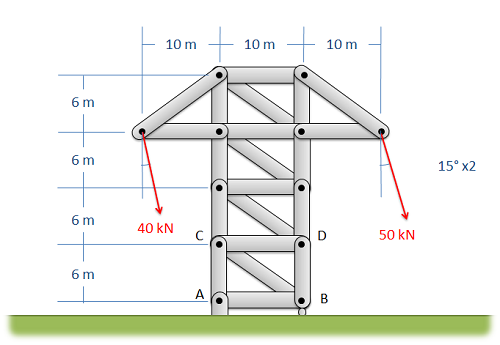
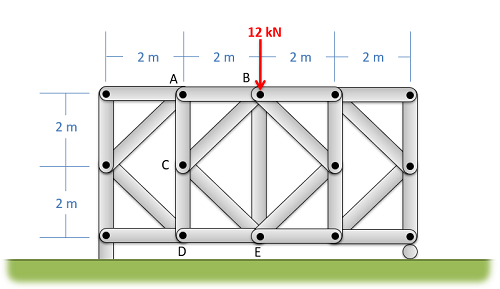
In some cases, you will need to determine the forces acting in a few members of a truss, but you will find that there is no one cut you can make with the method of sections that goes through all the members you need to solve for. In cases such as this, the method of sections may not be enough, but solving for everything with the method of joints may be overkill. In these cases, we may resort to one of the two following strategies to extend the method of sections beyond it's base process.
The first strategy we can use to extend the method of sections is to simply make a second cut and employ the method of sections again. In this strategy, start by using the method of sections normally to solve for some of the forces we are looking for. After making this first cut, we will repeat the process with a second cut, making sure to cut through the rest of the members that we wish to solve for in this second cut. Additionally, this second cut can travel through more than three members, so long as it does not travel through three unsolved members. Anything we solved for in the first round can be treated as a known value, and does not need to be solved for again.
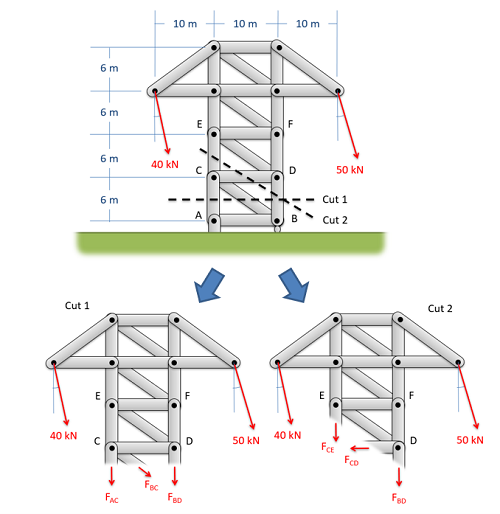
The second strategy to extend the method of sections, is to start with the method of sections, then to use the method of joints to work out from the initial cut. In this strategy, start by using the method of sections normally to solve for some of the forces we are looking for. After making the initial cut, we will switch to the method of joints, by picking a joint near the cut for analysis. For each joint we choose, just make sure there are no more than two unknowns to solve for. Continue analyzing joints until you have all the unknown forces you are looking for.