The Equations of Motion with Rectangular Coordinates
To start our discussion of kinetics in two dimensions, we will examine Newton's Second Law as applied to a fixed coordinate system. In its basic form, Newton's Second Law states that the sum of the forces on a body will be equal to mass of that body times the rate of acceleration. For bodies in motion, we can write this relationship out as the equation of motion.
| \[\sum \vec{F}=m*\vec{a}\] |
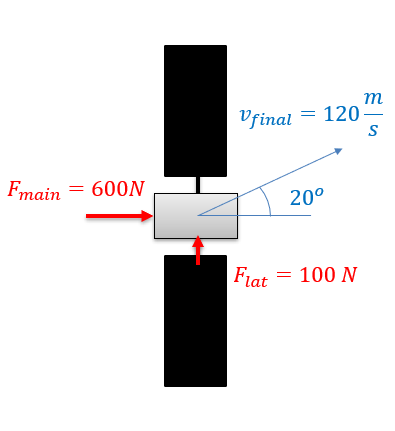
With rectangular coordinates in two dimensions, we will break this single vector equation into two separate scalar equations. To solve the equations, we simply break any given forces and accelerations down into x and y components using sines and cosines and plug those known values in. With two equations, we should be able to solve for up to two unknown force or acceleration terms.
| \[\sum F_{x}=m*a_{x}=m*\ddot{x}\] |
| \[\sum F_{y}=m*a_{y}=m*\ddot{y}\] |
Just as with a single dimension, the equations of motion are often used in conjunction with the kinematics equations, which relate positions, velocities and accelerations as discussed in the previous chapter. Depending on the problem being examined, the kinematics equations may need to be examined either before or after the kinetics equations.
Rectangular coordinates can be used in any kinetics problem, however they work best with problems where the forces do not change direction over time. Projectile motion is a good example of this, because the gravity force will maintain a constant direction, as opposed to the thrust force on a turning plane, where the thrust force changes direction with the plane.