Centroids and Area Moments of Inertia for 2D Shapes
| Shape with Area and Centroid Location Shown | Rectangular Area Moments of Inertia | Polar Area Moments of Inertia |
Rectangle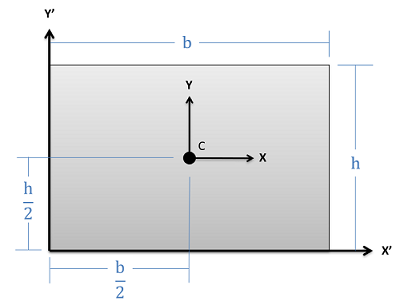 \[Area=bh\] \[Area=bh\] |
\[I_{x}=\frac{1}{12}bh^{3}\] \[I_{y}=\frac{1}{12}b^{3}h\] | \[J_{z}=\frac{1}{12}bh(b^{2}+h^{2})\] |
Right Triangle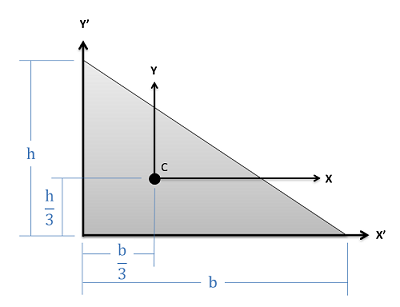 \[Area=\frac{1}{2}bh\] \[Area=\frac{1}{2}bh\] |
\[I_{x}=\frac{1}{36}bh^{3}\] \[I_{y}=\frac{1}{36}b^{3}h\] \[I_{x'}=\frac{1}{12}bh^{3}\] \[I_{y'}=\frac{1}{12}b^{3}h\] |
|
Triangle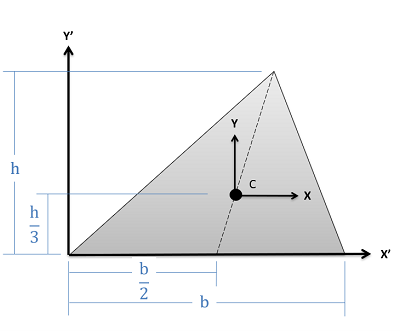 \[Area=\frac{1}{2}bh\] \[Area=\frac{1}{2}bh\] |
\[I_{x}=\frac{1}{36}bh^{3}\] \[I_{x'}=\frac{1}{12}bh^{3}\] |
|
Circle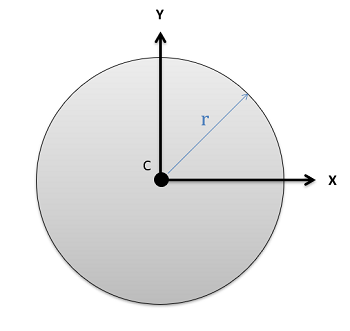 \[Area=\pi r^{2}\] \[Area=\pi r^{2}\] |
\[I_{x}=\frac{\pi}{4}r^{4}\] \[I_{y}=\frac{\pi}{4}r^{4}\] | \[J_{z}=\frac{\pi}{2}r^{4}\] |
Circular Annulus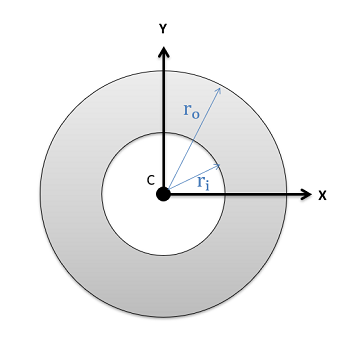 \[Area=\pi (r_{o}^{2}-r_{i}^{2})\] \[Area=\pi (r_{o}^{2}-r_{i}^{2})\] |
\[I_{x}=\frac{\pi}{4}(r_{o}^{4}-r_{i}^{4})\] \[I_{y}=\frac{\pi}{4}(r_{o}^{4}-r_{i}^{4})\] | \[J_{z}=\frac{\pi}{2}(r_{o}^{4}-r_{i}^{4})\] |
Semicircle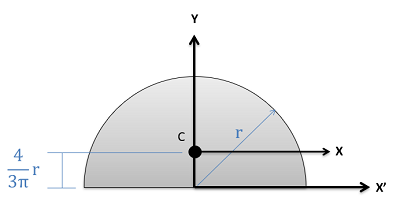 \[Area=\frac{\pi}{2} r^{2}\] \[Area=\frac{\pi}{2} r^{2}\] |
\[I_{x}=\left(\frac{\pi}{8}-\frac{8}{9\pi}\right) r^{4}\] \[I_{y}=\frac{\pi}{8}r^{4}\] \[I_{x'}=\frac{\pi}{8}r^{4}\] |
\[J_{z}=\left(\frac{\pi}{4}-\frac{8}{9\pi}\right) r^{4}\] |
Quarter Circle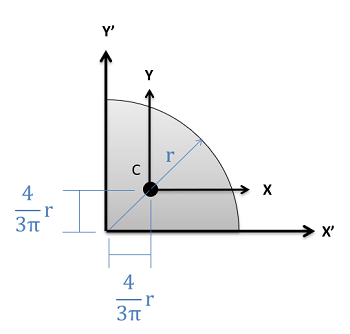 \[Area=\frac{\pi}{4} r^{2}\] \[Area=\frac{\pi}{4} r^{2}\] |
\[I_{x}=\left(\frac{\pi}{16}-\frac{4}{9\pi}\right) r^{4}\] \[I_{y}=\left(\frac{\pi}{16}-\frac{4}{9\pi}\right) r^{4}\] \[I_{x'}=\frac{\pi}{16}r^{4}\] \[I_{y'}=\frac{\pi}{16}r^{4}\] |
\[J_{z}=\left(\frac{\pi}{8}-\frac{8}{9\pi}\right) r^{4}\] |
Ellipse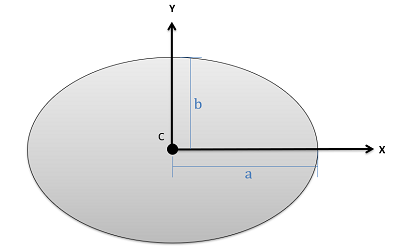 \[Area=\pi ab\] \[Area=\pi ab\] |
\[I_{x}=\frac{\pi}{4}ab^{3}\] \[I_{y}=\frac{\pi}{4}a^{3}b\] | |
Circular Sector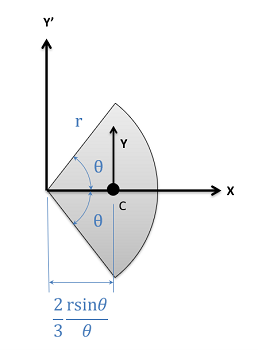 \[Area=\theta r^2\] \[Area=\theta r^2\] |
\[I_{x}=\frac{1}{4} \left(\theta - \frac{1}{2}\sin{2\theta} \right) r^{4}\] | |
Quarter Circle Arc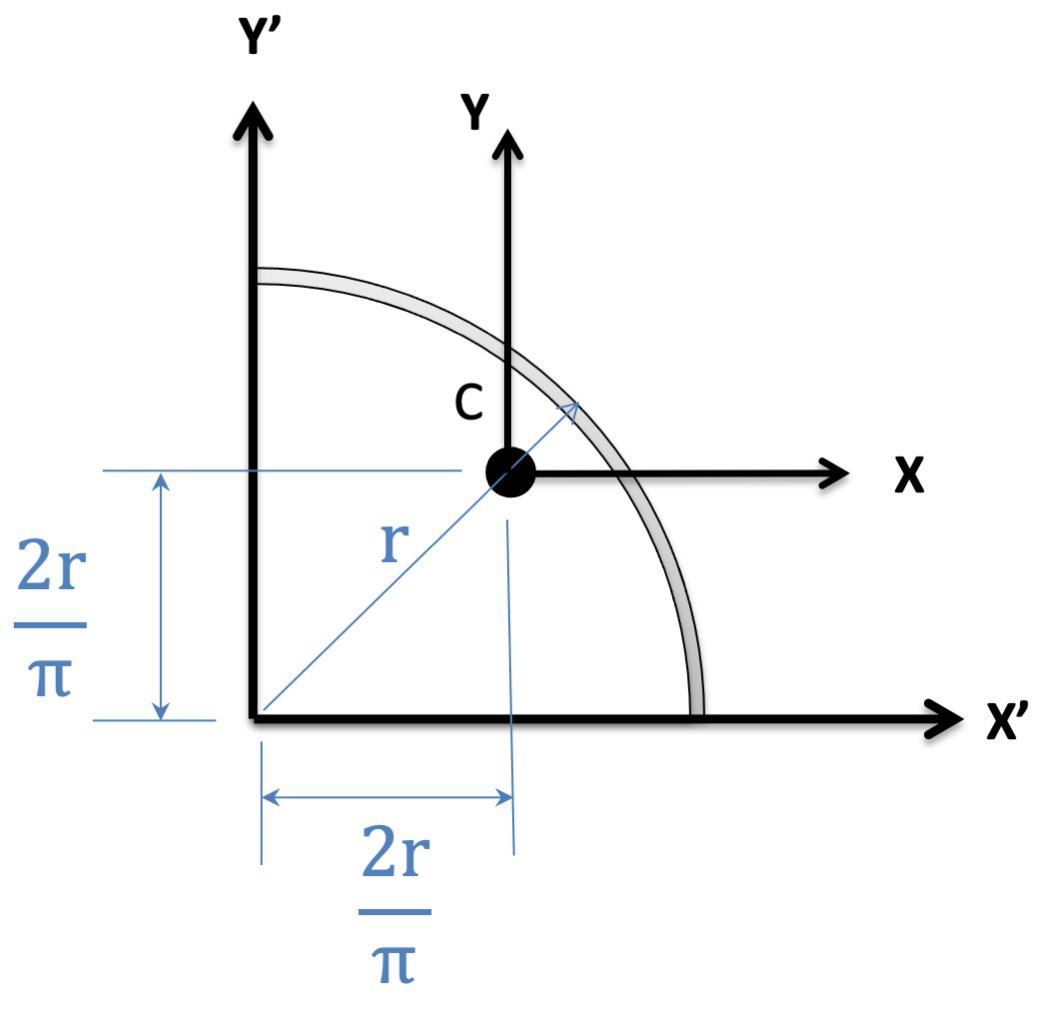 \[Length=\frac{\pi}{2} r\] \[Length=\frac{\pi}{2} r\] |
||
Semicircle Arc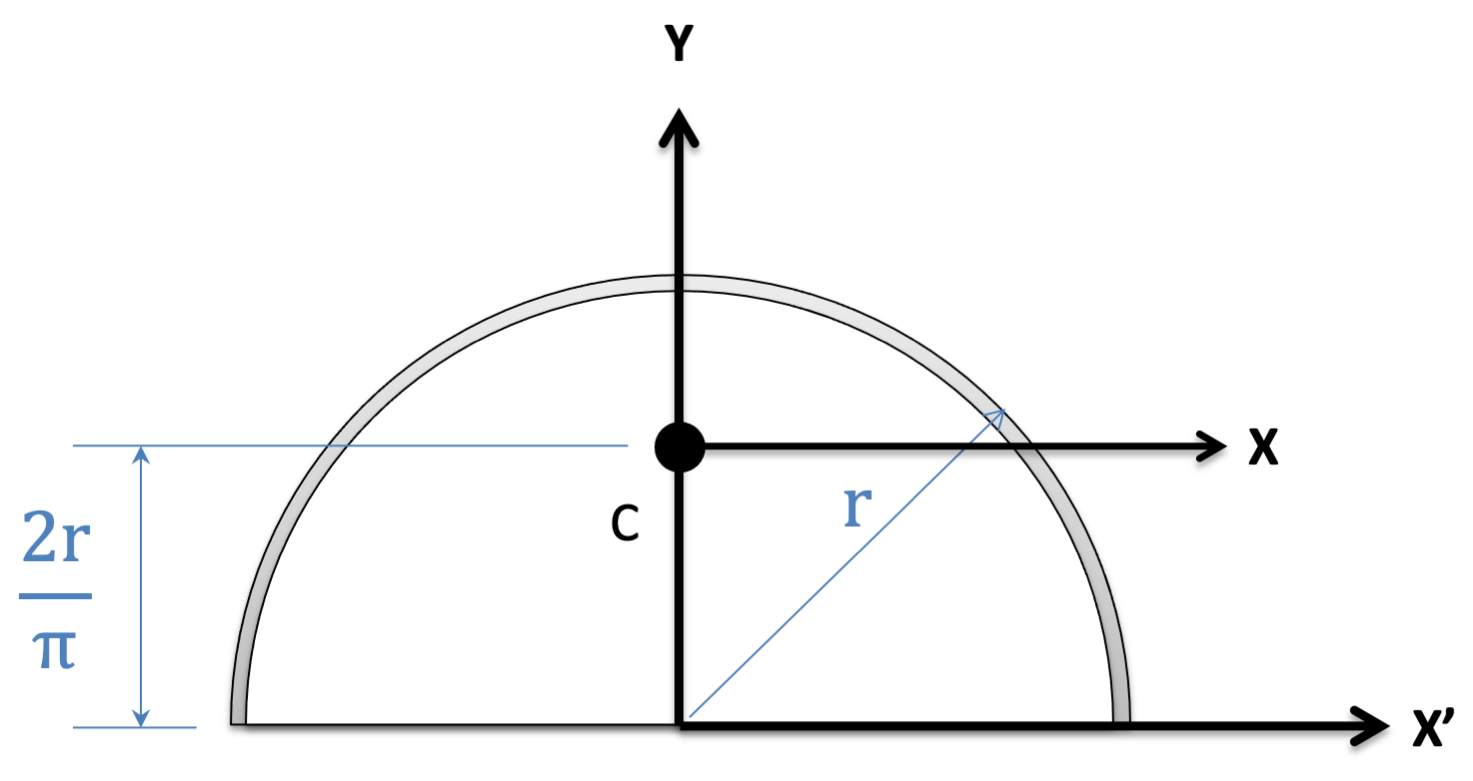 \[Length=\pi r\] \[Length=\pi r\] |
||
Circular Arc Segment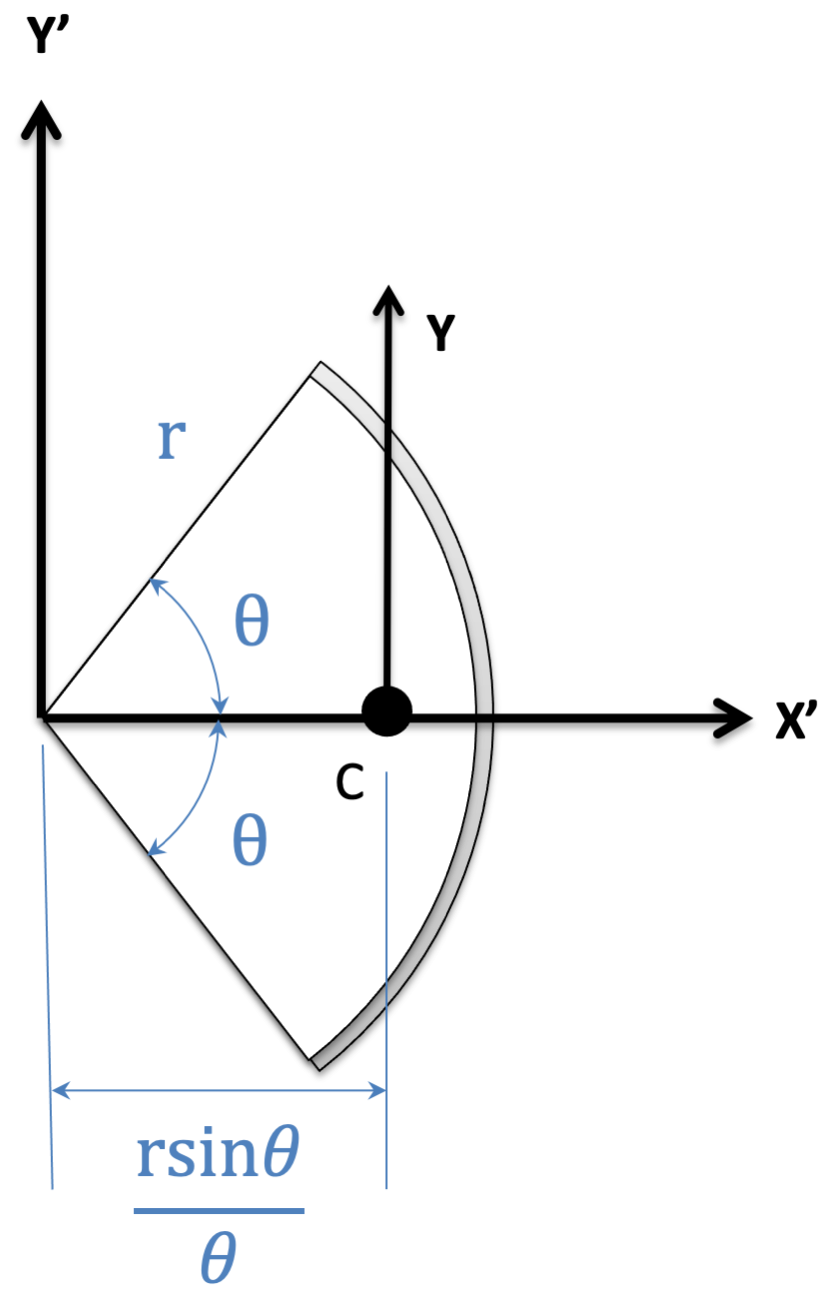 \[Length=2 \theta r\] \[Length=2 \theta r\] |
||
Parabolic Area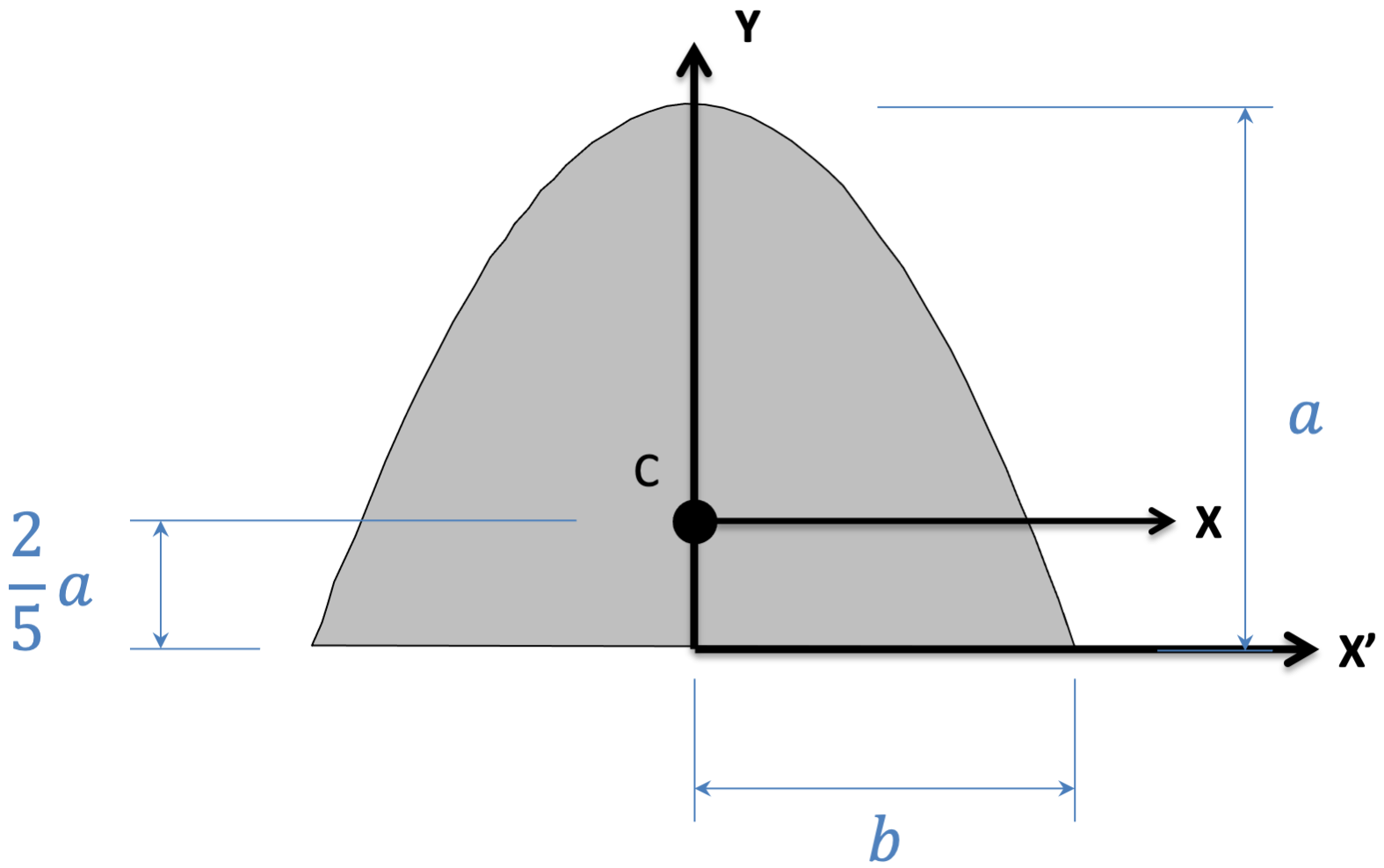 \[Area = \frac{4}{3} ab \] \[Area = \frac{4}{3} ab \] |