Center of Mass and Mass Moments of Inertia for Homogeneous Bodies
| Shape with Volume and Center of Mass Location Shown | Mass Moments of Inertia |
Slender Rod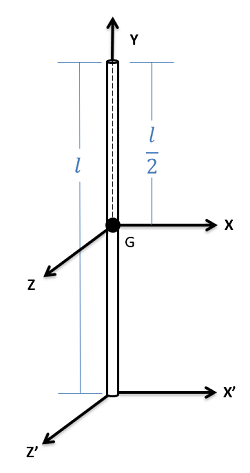
|
\[I_{xx}=I_{zz}=\frac{1}{12}ml^{2}\] \[I_{yy}=0\] \[I_{xx'}=I_{zz'}=\frac{1}{3}ml^{2}\] |
Flat Rectangular Plate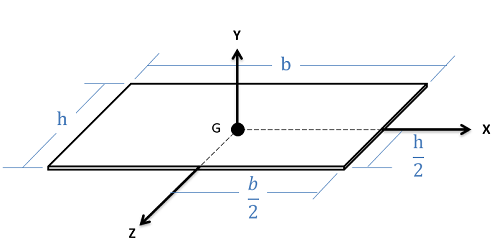
|
\[I_{xx}=\frac{1}{12}mh^{2}\] \[I_{yy}=\frac{1}{12}m(h^{2}+b^{2})\] \[I_{zz}=\frac{1}{12}mb^{2}\] |
Flat Circular Plate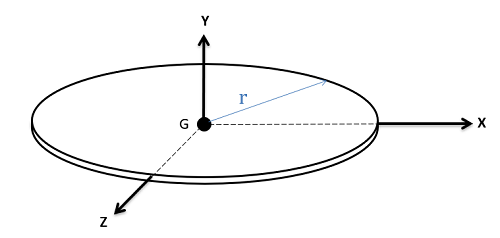
|
\[I_{xx}=I_{zz}=\frac{1}{4}mr^{2}\] \[I_{yy}=\frac{1}{2}mr^{2}\] |
Thin Circular Ring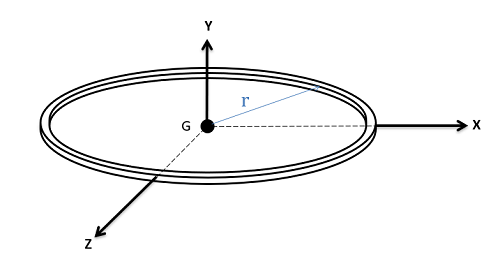
|
\[I_{xx}=I_{zz}=\frac{1}{2}mr^{2}\] \[I_{yy}=mr^{2}\] |
Rectangular Prism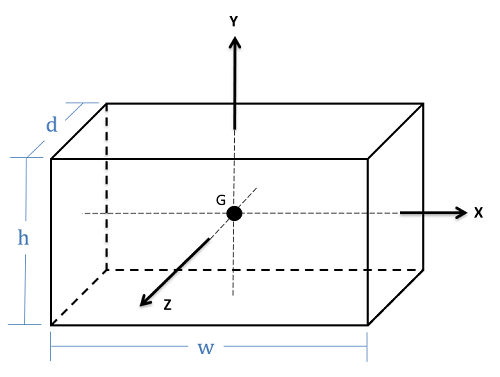 \[Volume=dhw\]
\[Volume=dhw\]
|
\[I_{xx}=\frac{1}{12}m(h^{2}+d^{2})\] \[I_{yy}=\frac{1}{12}m(d^{2}+w^{2})\] \[I_{zz}=\frac{1}{12}m(h^{2}+w^{2})\] |
Cylinder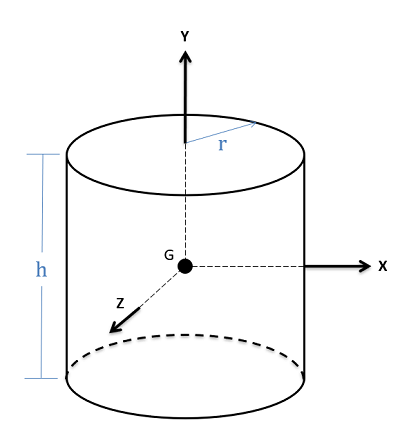 \[Volume=\pi r^{2}h\]
\[Volume=\pi r^{2}h\]
|
\[I_{xx}=I_{zz}=\frac{1}{12}m(3r^{2}+h^{2})\] \[I_{yy}=\frac{1}{2}mr^{2}\] |
Thin Cylindrical Shell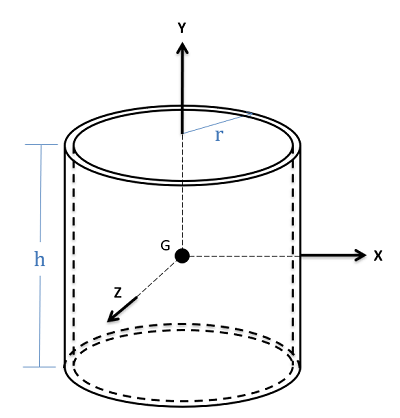 |
\[I_{xx}=I_{zz}=\frac{1}{6}m(3r^{2}+h^{2})\] \[I_{yy}=mr^{2}\] |
Half Cylinder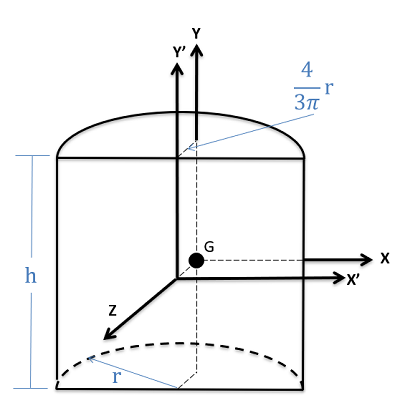 \[Volume=\frac{1}{2}\pi r^{2}h\]
\[Volume=\frac{1}{2}\pi r^{2}h\]
|
\[I_{xx}=I_{zz}=\left( \frac{1}{4}-\frac{16}{9\pi^{2}} \right)mr^{2}+\frac{1}{12}mh^{2}\] \[I_{yy}=\left(\frac{1}{2}-\frac{16}{9\pi^{2}}\right)mr^{2}\] \[I_{xx'}=I_{zz'}=\frac{1}{12}m(3r^{2}+h^{2})\] \[I_{yy'}=\frac{1}{2}mr^{2}\] |
Sphere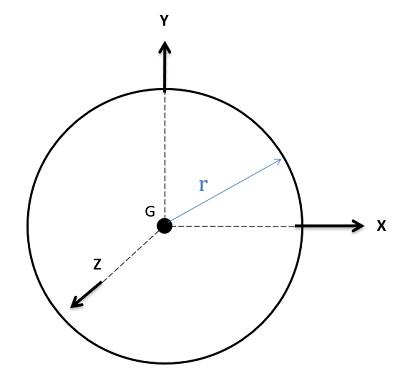 \[Volume=\frac{4}{3}\pi r^{3}\]
\[Volume=\frac{4}{3}\pi r^{3}\]
|
\[I_{xx}=I_{yy}=I_{zz}=\frac{2}{5}mr^{2}\] |
Spherical Shell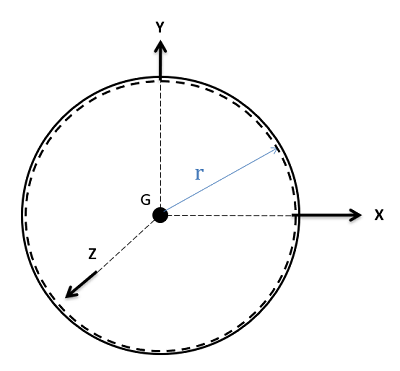
|
\[I_{xx}=I_{yy}=I_{zz}=\frac{2}{3}mr^{2}\] |
Hemisphere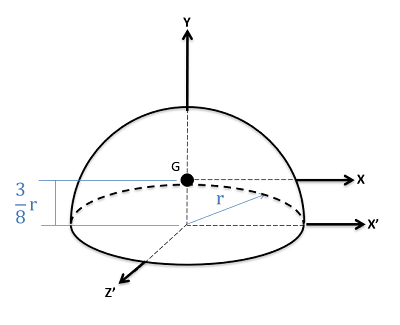 \[Volume=\frac{2}{3}\pi r^{3}\]
\[Volume=\frac{2}{3}\pi r^{3}\]
|
\[I_{xx}=I_{zz}=\frac{83}{320}mr^{2}\] \[I_{yy}=\frac{2}{5}mr^{2}\] \[I_{xx'}=I_{zz'}=\frac{2}{5}mr^{2}\] |
Hemispherical Shell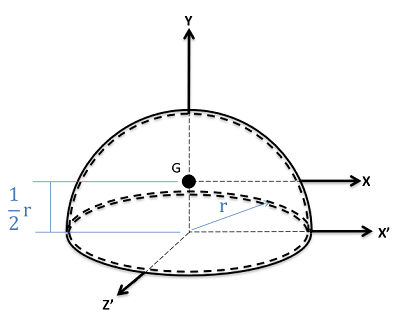
|
\[I_{xx}=I_{zz}=\frac{5}{12}mr^{2}\] \[I_{yy}=\frac{2}{3}mr^{2}\] \[I_{xx'}=I_{zz'}=\frac{2}{3}mr^{2}\] |
Right Circular Cone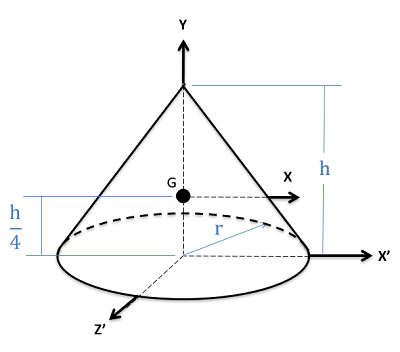 \[Volume=\frac{1}{3}\pi r^{2}h\]
\[Volume=\frac{1}{3}\pi r^{2}h\]
|
\[I_{xx}=I_{zz}=\frac{3}{80}m(4r^{2}+h^{2})\] \[I_{yy}=\frac{3}{10}mr^{2}\] \[I_{xx'}=I_{zz'}=\frac{1}{20}m(3r^{2}+2h^{2})\] |