Buoyancy
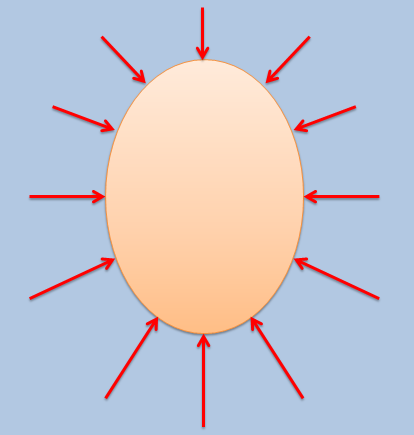
Objects that are submerged or partially submerged in a liquid will experience hydrostatic pressures acting on all surfaces in contact with the liquid as shown in the figure on the right. The forces acting on the sides tend to cancel each other out, being equal and opposite. The magnitude of the pressure increases with depth though, leading to larger hydrostatic forces on the bottom surface pushing an object up than hydrostatic forces on the top surface, pushing the object down. This unequal set of forces leads to a net, upward hydrostatic force acting on the object called buoyancy.
Adding together all of the distributed forces acting on the surfaces of the object is tedious, but luckily there is a shortcut to getting the net buoyancy force acting on an object. Imagine we fill a very thin walled water balloon with water and submerge this in a larger pool of water, this water in the balloon is the same density as the water surrounding it and will therefore be neutrally buoyant. This means the water balloon will not sink or float in the larger pool. The water balloon is in static equilibrium, and only has two forces acting on it (the weight due to gravity and the buoyancy force). These two forces must be equal and opposite for the object to be in equilibrium, therefore the net buoyancy force will be equal and opposite to the weight of the balloon as shown in example B in the picture below..
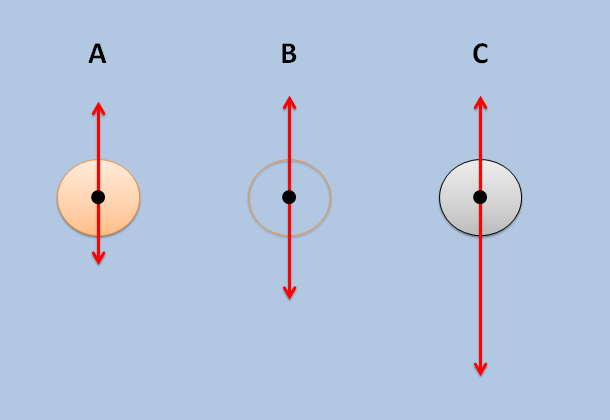
If we replaced the water balloon with either a piece of foam (A) or a piece of metal (C) that is exactly the same size and shape as the original balloon, it would experience the same hydrostatic pressures, and therefore experience the same buoyancy force as the original water balloon. The reason some things sink and some float is because the weight is more or less than the original water balloon.
The weight of the water in the balloon is equal to the density of the water, times the gravitational constant g, times the volume of the water balloon. This will also be magnitude of the buoyancy force.
\[ \mathrm{ F_B = \rho*g*V }\]Where \( \mathrm{F_B} \) is the buoyancy force,
\( \mathrm{\rho} \) is the density of the liquid the object is submerged in,
\( \mathrm{g} \) is pull of gravity (9.81 N/kg on earth)
and \( \mathrm{V} \) is the volume of the object that lies below the surface of the water
This force will act through the center of gravity of the volume of the object that is below water, having the same line of action as the gravity force for any object that is in equilibrium while floating or submerged.
Worked Problems
Worked Problem 1:
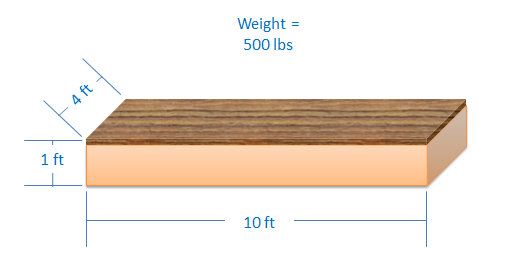
A floating dock is built out of a wood surface on a foam base. It is built to the dimensions shown below and has a total weight of 500 pounds. If the dock is placed in water, how high will the surface of the dock be off the surface of the water? How many pounds can the dock support before sinking below the surface of the water?
| Work | Comments |
|
\[ \mathrm{
500 lbs = \rho g V
}\]
|
To find how far above the surface of the water the dock floats, the weight of the dock and the buoyancy force must be balanced (equal and opposite). The weight is given at 500 lbs, so we set this equal to the equation for the buoyancy force. |
|
\[ \mathrm{
V = \frac{500 lbf}{\rho g}
}\]
\[ \mathrm{
V = \frac{500 lbf}{62.4\frac{lbm}{ft^3} 1\frac{lbf}{lbm}}
}\]
\[ \mathrm{
V = 8.01 ft^3
}\]
|
By solving for V, we can find the volume of the dock below the surface of the water. We simply look up and plug in values for g and \( \mathrm{\rho} \). |
|
\[ \mathrm{
V = l * w * h = 8.01 ft^3
}\]
\[ \mathrm{
V = 10 * 4 * h = 8.01 ft^3
}\]
\[ \mathrm{
h = .2 ft
}\]
|
Next, we use the submerged volume to find the submerged height. |
|
\[ \mathrm{
\text{height above the water} = .8 ft = 9.6in
}\]
|
And we use that to find out how high the surface of the dock is above the surface of the water. |
|
\[ \mathrm{
F_B = \rho g V
}\]
|
Next we want to find how out what the maximum load on the dock is before it becomes submerged. To do this we want to find out what the buoyancy force is if the dock is completely submerged. |
|
\[ \mathrm{
F_B = 62.4\frac{lbm}{ft^3} 1\frac{lbf}{lbm} 40\text{ft}^3
}\]
\[ \mathrm{
F_B = 2496\text{ lbf}
}\]
|
We plug in the values and find the buoyancy force if the dock is completely submerged. |
|
\[ \mathrm{
\text{ Maximum load the dock can support} = 2496 - 500 = 1996 \text{ lbf}
}\]
|
We subtract the weight of the dock itself and we are left with the maximum weight the dock can support. |
 |
| Author: Jacob Moore has liscenced this work under a Creative Commons Attribution-NonCommercial 3.0 Unported License. |