Hydrostatic Pressure on Curved Surfaces
If a liquid is in contact with a surface, it will exert distributed hydrostatic pressure on that surface. On the Hydrostatic Pressure on a Flat Surface page we learned how to integrate this distributed load to find the equivalent point load. Integrating this load over a non-flat surface is much more difficult because of the changing direction of the force, but we can redefine the body being analyzed to make the process of finding the equivalent point load for the hydrostatic pressure on any non-flat surface easier.
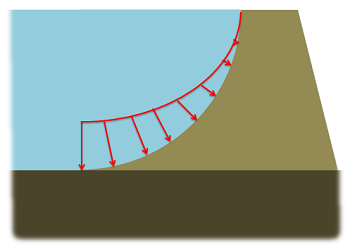
Hydrostatic pressure on a curved surface.
|
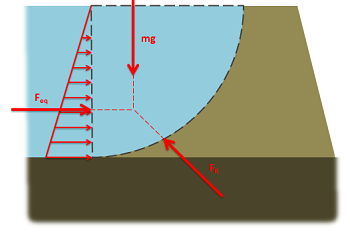
A free body diagram of the volume of water above the curved surface.
|
The images above show hydrostatic pressure acting on the curved surface of a dam. The image on the left shows the pressure acting on the surface. The magnitude of the pressure increases with depth and always acts perpendicular to the surface. Finding the equivalent point load for this distributed force directly is a very difficult task. Instead, we analyze the body of water over top of the surface we are trying to analyze (in this case the quarter circle outlined with the dotted black line). This body of water is in equilibrium, and has only three forces acting on it.
- The hydrostatic pressure acting on the flat side of the defined volume of liquid. This is simply a hydrostatic pressure acting on a flat surface.
- The weight of the liquid in the defined volume.
- The reaction force from the surface in contact with the liquid.
Being able to determine the hydrostatic pressure on the flat surface and the weight of the liquid in the prescribed volume, you should be able to solve for the reaction force. The equivalent point load the liquid exerts on the curved surface is equal and opposite to the reaction force (the equivalent point load for the distributed force shown in the image on the left, is equal and opposite to the reaction force you can solve for).
Worked Problems
Worked Problem 1:
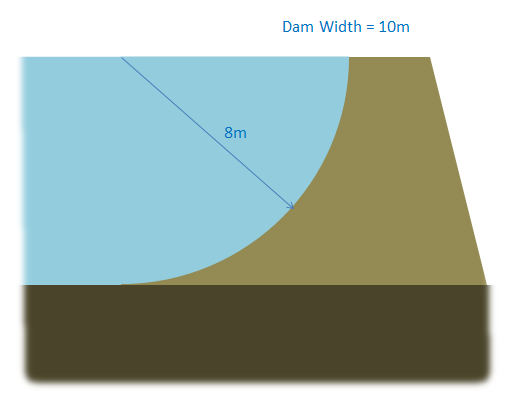
The dam shown below has a cylindrical surface with a radius of 8 meters. If water is built up to the top of the dam, what is the equivalent point load of the water pressing against the dam.
| Work | Comments |
|
To solve this problem, we analyze the body of water in the quarter of a cylinder above the dam itself. We will solve for the use the hydrostatic pressures acting on the flat surface and the weight of the water to solve for the reaction force. |
|
\[ \mathrm{
F_{eq} = w \rho g cos(\theta)\int x * dx
}\]
\[ \mathrm{
x_{eq} = \frac{w\rho g cos(\theta)}{F_{eq}}* \int\left( x^2 * dx\right)
}\]
|
First we will solve for the hydrostatic pressure on the flat surface on the left. To do this we use the equations to the left to solve for \(\mathrm{F_{eq}}\) and \(\mathrm{x_{eq}}\). |
|
\[ \mathrm{
F_{eq} = 10 \text{ m} * 1000 \frac{kg}{m^3} 9.81 \frac{N}{kg} \int_0^8 x * dx
}\]
\[ \mathrm{
F_{eq} = 3139 \text{ kN}
}\]
\[ \mathrm{ x_{eq} = \frac{10 \text{ m} * 1000 \frac{kg}{m^3} 9.81 \frac{N}{kg}}{3139 \text{ kN}}* \int_0^8 x^2 * dx }\] \[ \mathrm{ x_{eq} = 5.33 \text{ m} }\] |
We solve those equations and find Feq and xeq. |
|
\[ \mathrm{
m*g = \rho*g*V
}\]
\[ \mathrm{
V = \frac{1}{4}*\pi*r^2*w
}\]
\[ \mathrm{
V = \frac{1}{4}*\pi*r^2*w
}\]
\[ \mathrm{
V = 502.7 \text{ m}^3
}\]
\[ \mathrm{
m*g = 1000 \frac{kg}{m^3}*9.81 \frac{N}{kg}*502.7 \text{ m}^3
}\]
\[ \mathrm{
m*g = 4931 \text{ kN}
}\]
\[ \mathrm{ COM = \frac{4}{3*\pi}*r = 3.40 \text{ m} }\] |
Next we need to determine the weight and center of mass of the body of water. The weight is simply the volume times the density of water times the pull of gravity. The center of mass can be looked up in a table. |
|
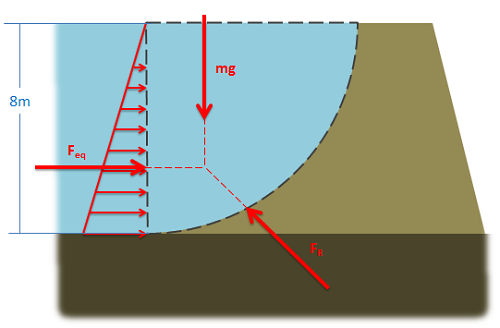
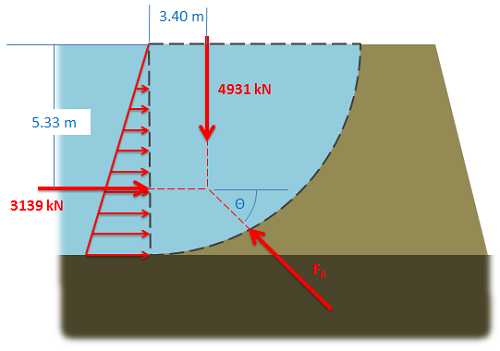
We then draw in the known forces and distances on the original diagram. |
|
\[ \mathrm{
\sum{F_x}=0= 3139\text{ kN} - cos(\theta)*F_R
}\]
\[ \mathrm{
\sum{F_y}=0= -4931\text{ kN} + sin(\theta)*F_R
}\]
\[ \mathrm{ F_R = 5845\text{ kN} }\] \[ \mathrm{ \theta = 57.5^o }\] |
We use this new diagram to write out the equations of static equilibrium for the body of water. We will use the sum of forces in the x and y directions to solve for the magnitude of \(\mathrm{F_R}\) and the angle \(\mathrm{\theta}\). |
|
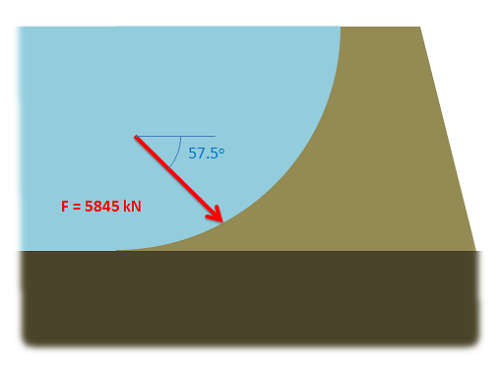
The equivalent point load is equal and opposite in direction. Here is the equivalent point load (magnitude and direction) drawn on the original diagram. |
 |
| Author: Jacob Moore has liscenced this work under a Creative Commons Attribution-NonCommercial 3.0 Unported License. |