Multi-Body Kinetics
In cases where multiple connected rigid bodies are undergoing some sort of motion, we can extend our analysis of general planar motion to this multi-body situation. In these cases, which we will call multi-body kinetics problems, we will analyze each body independently as we did for general planar motion, but we will also need to pay attention to the Newton's Third Law pairs. Each body will have forces and/or moments exerted on it by the surrounding bodies, and it will exert equal and opposite forces/moments back through those same connections.

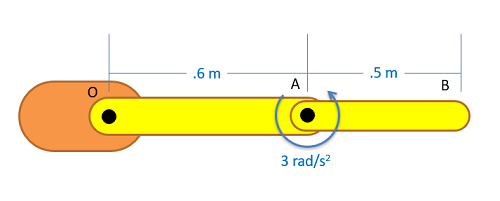
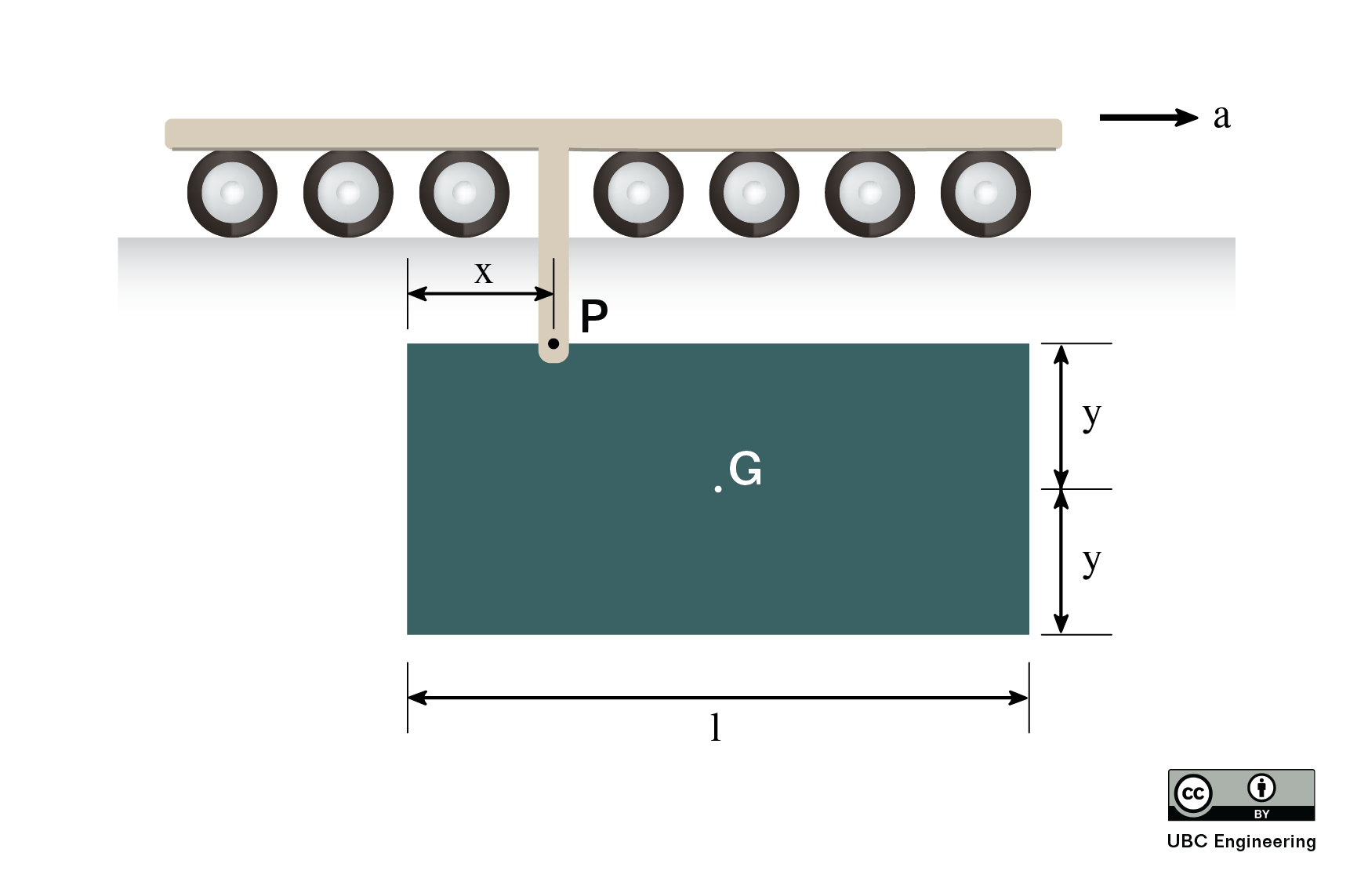
To analyze a multi-body system, we will start by drawing a free body diagram of each body in motion. Be sure to identify the center of mass, as well as identifying all known and unknown forces, and known and unknown moments acting on the body. When drawing forces and moments at connection points, be sure to make the forces and moments equal and opposite on the connected body to satisfy Newton's Third Law. It is also sometimes helpful to label any key dimensions as well as using dashed lines to identify any known accelerations or angular accelerations. Often, you will need to solve a kinematics problem using absolute motion analysis or relative motion analysis in order to determine the accelerations of the centers of mass and the angular accelerations for each body. Make sure all these accelerations are with respect to ground.
Next we move onto identifying the equations of motion for each body in the system. In two dimensions, we will use the same three equations we used for general planar motion. Be sure to find the the accelerations of all the centers of masses, find all moments about the center of mass, and take the mass moments of inertia about the center of mass of each body.
| \[\sum F_{x}=m*a_{x}\] |
| \[\sum F_{y}=m*a_{y}\] |
| \[\sum M_{G}=I_{G}*\alpha\] | or (taking moments about the ICZV) |
| \[\sum \vec{M}_{IC}=I_{IC}\vec{\alpha}\] | or (taking moments about any point, P, on the body) |
| \[ \sum \vec{M}_{P}=I_{G}\vec{\alpha}+ \vec{r}_{G/P} \times m \vec{a}_G \] | or |
| \[ \sum \vec{M}_{P}=I_{P}\vec{\alpha}+ \vec{r}_{G/P} \times m \vec{a}_P \] |
Plugging the known forces, moments, and accelerations into the above equations we can solve for up to three unknowns per body. If more than three unknowns exist in any one set of equations, you will need to start with an adjacent body. Once unknown forces and moments are determined on one body, they can become knowns on the connected body, reducing the number of unknowns to solve for.