Viscous Damped Harmonic Forced Vibrations
As described in the previous section, many vibrations are caused by an external harmonic forcing function (such as rotating unbalance). While we assumed that the natural vibrations of the system eventually damped out somehow, leaving the forced vibrations at steady-state, by explicitly including viscous damping in our model we can evaluate the system through the transient stage when the natural vibrations are present.
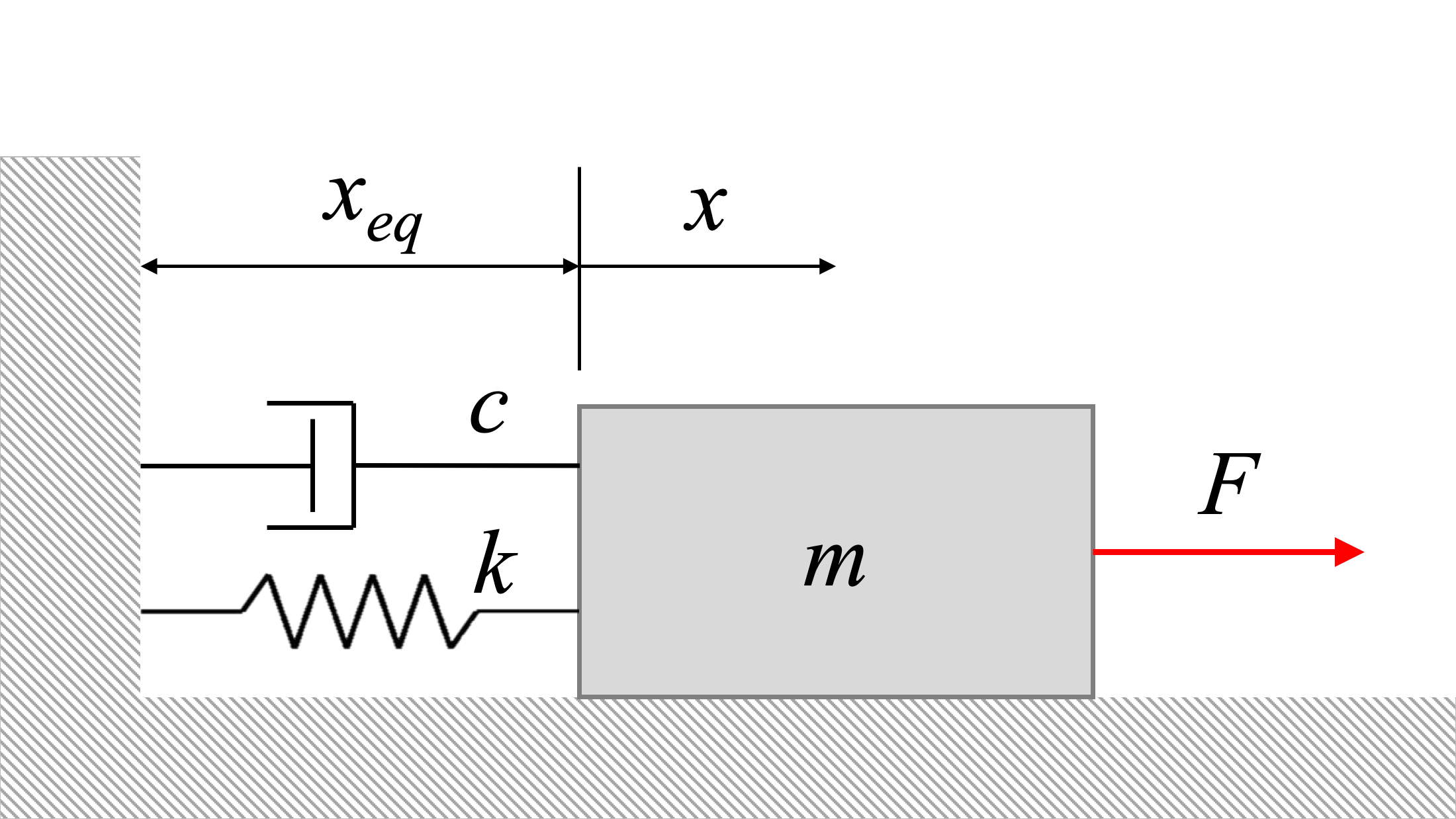
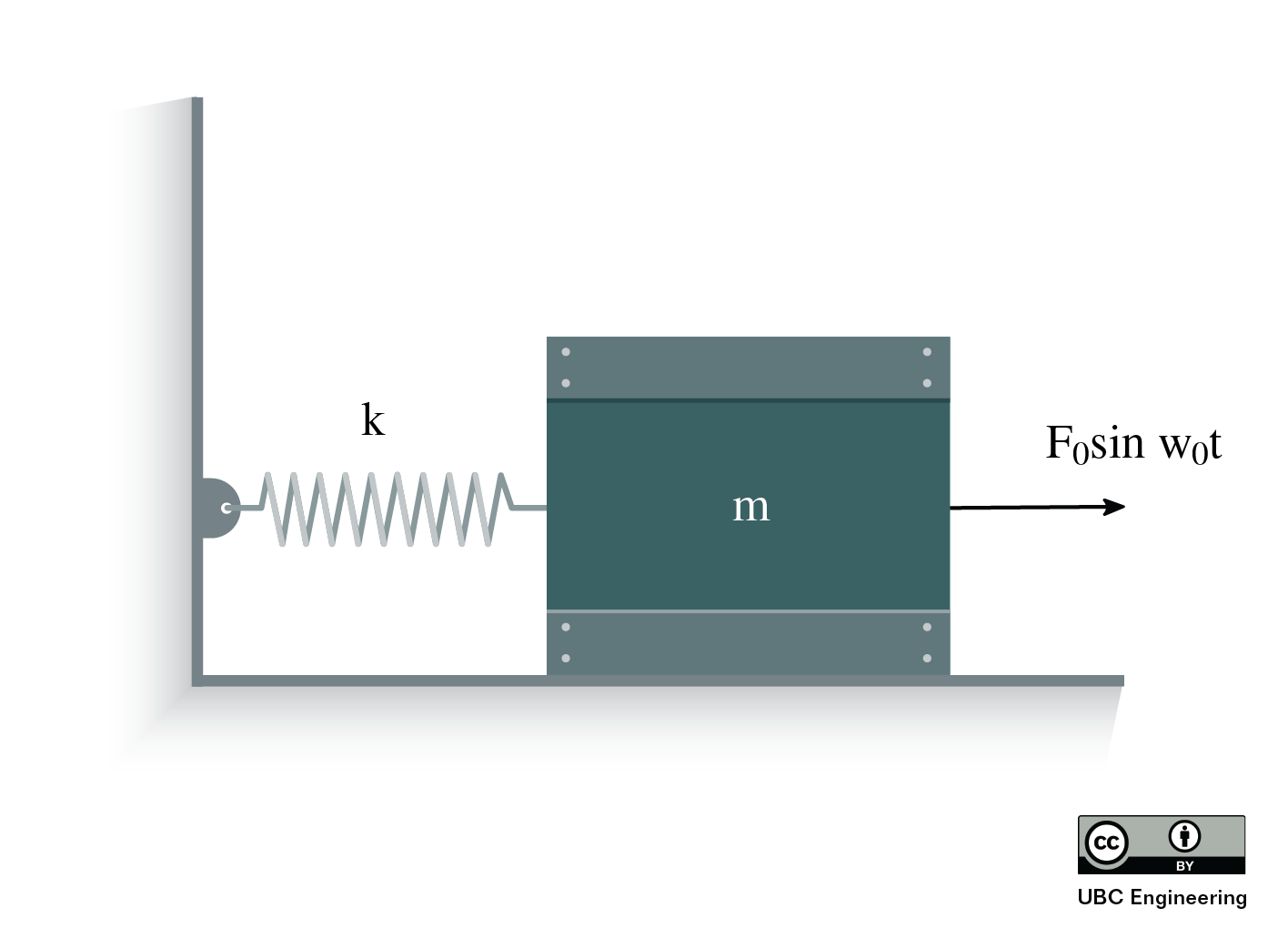
Consider the system above. The equation of the system becomes:
| \[ m {\ddot{x}} + c \dot{x} + k {x} = F_0 \sin \omega_0 t \] |
| \[ \Rightarrow \, {\ddot{x}} + \frac{c}{m} \dot{x} + \frac{k}{m} {x} = \frac{F_0}{m} \sin \omega_0 t \] |
Because the natural vibrations will damp out with friction (as mentioned in undamped harmonic vibrations), we will only consider the particular solution. This particular solution will have the form:
| \[ x_p(t) = X' \sin (\omega_0 t - \phi ')\] |
After solving, we determine that the expressions for X' and ϕ' are:
| \[ X' = \frac{\displaystyle \frac{F_0}{k}}{\sqrt{\left[ 1- \left( \displaystyle \frac{\omega_0}{\omega_n} \right)^2 \right]^2 + \left[ \displaystyle 2 \frac{c}{c_c} \frac{\omega_0}{\omega_n} \right]^2 }} \] |
| \[ \phi'=\tan^{-1} \left[ \displaystyle \frac{ \displaystyle 2 \frac{c}{c_c} \frac{\omega_0}{\omega_n} }{ \displaystyle 1- \left( \displaystyle\frac{\omega_0}{\omega_n} \right)^2} \right] \] |
The magnification factor now becomes:
| \[ MF = \frac{X'}{\displaystyle \frac{F_0}{k}} = \frac{1}{\sqrt{\left[ 1- \left( \displaystyle \frac{\omega_0}{\omega_n} \right)^2 \right]^2 + \left[ \displaystyle 2 \frac{c}{c_c} \frac{\omega_0}{\omega_n} \right]^2 }} \] |
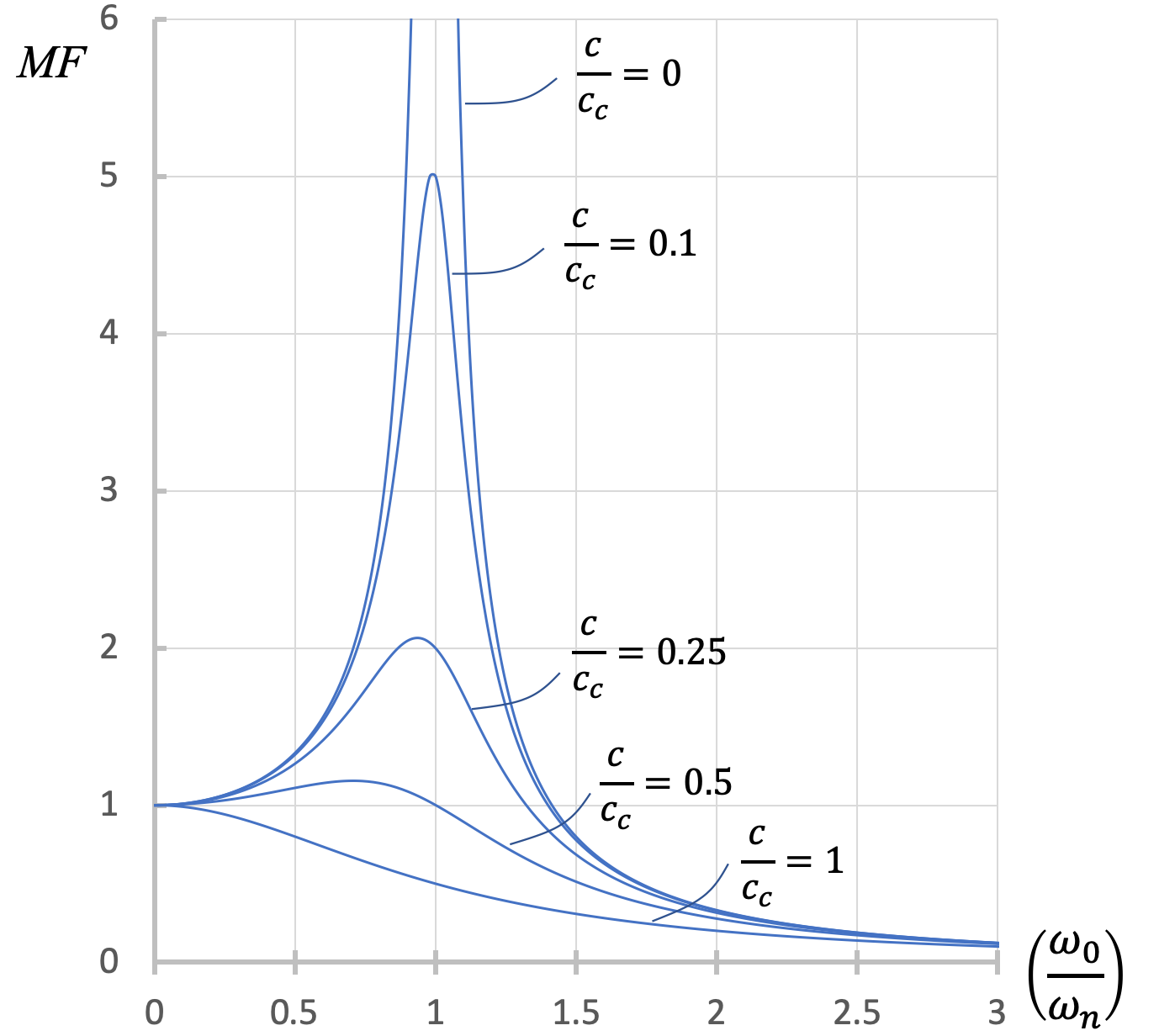
From the figure above, we can see that the extreme amplitudes at resonance only occur when the damping ratio = 0 and the ratio of frequencies is 1. Otherwise, damping inhibits the out-of-control vibrations that would otherwise be seen at resonance.