Internal Forces
So far in statics, we have focused on the external forces acting on on bodies. These external forces are the forces applied on one body by other surrounding bodies. Whenever we have external forces acting on a body though, a set of internal forces and internal moments will develop within the body to balance out the external forces. In order to understand how a body will deform and if it will break under loading, it is important to understand these internal forces and moments.
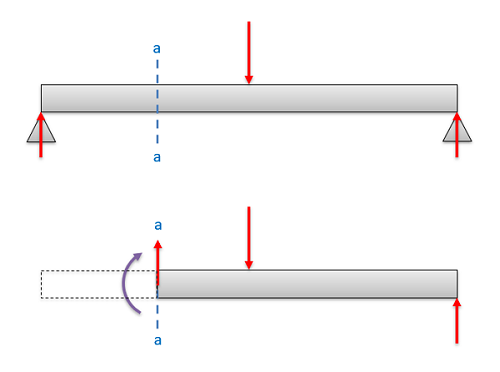
The first step in determining the internal forces, is to define the location we are looking at within the body. Usually this location is defined by examining a specific cross section that we are examining. It is important to clearly define this cross section early on, since the internal forces will vary from one cross section the next, even if all the external forces are the same.
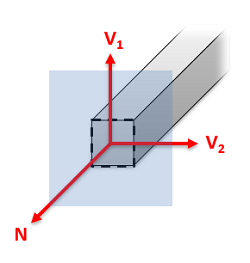
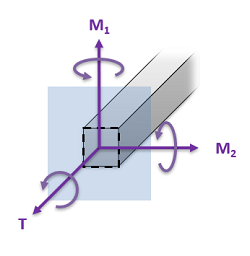
No matter how complex the external loading conditions, we will only have two possible types of internal forces at any given cross section and two types of internal moments at any given cross section. These forces and moments are...
- Normal Forces (also sometimes called axial forces) act perpendicular to the cross section being examined and will tend to stretch or compress the body.
- Shear Forces act parallel to the cross section and will tend to push deform the body along the cross section in the direction of the force.
- Torsional Moments are moments where the moment vector is perpendicular to the cross section being examined and will tend to twist the body.
- Bending Moments are moments where the moment vector is parallel to the cross section being examined and will tend to bend the body.
|
|
Determining Internal Forces and Moments
To determine the internal forces and moments in a body we have different approaches:
The first approach is just a static analysis of half of the body, similar to the approach used in the method of sections for trusses. Start by finding all external forces, draw a free body diagram of half of the body which is split at the cross section of interest, and then solve for all the unknown internal forces at the cross section. This method is usually faster for finding the forces and moments at a set location, though if you want to find the forces and moments at a second location you will need to do the analysis all over again.
The second approach is a graphical method that can be used to solve for the normal forces, shear forces, torsional moments, and bending moments across a range of cross sections. This method generally takes longer, and we can only graph one type of force or moment at a time, but it will allow us to graph the internal forces or moments along the entire length of the beam or shaft.