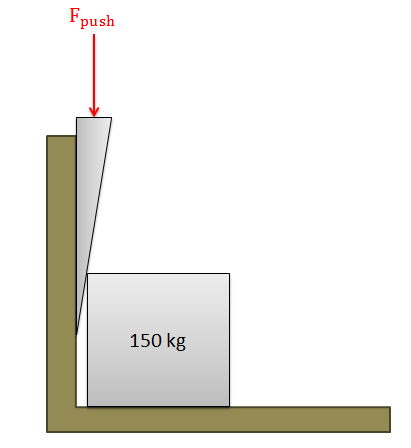
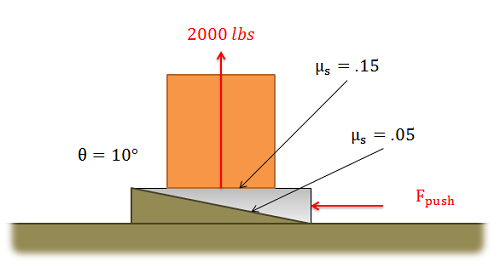
Wedges
A wedge is a thin wedge-shaped object that is used to force two objects apart or to force one object away from a close surface. Wedges have the effect of allowing users to create very large normal forces to move objects with relatively small input forces. The friction forces in wedge systems also tend to be very large though, and can reduce the effectiveness of wedges.
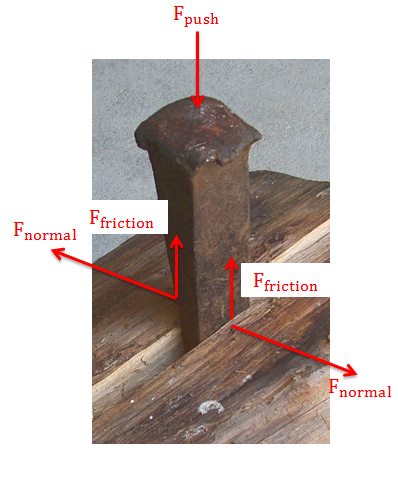
To analyze a wedge system we will need to draw free body diagrams of each of the bodies in the system (the wedge itself and any bodies the wedge will be moving). We need to be sure that we include the pushing force on the wedge, normal forces along any surfaces in contact, and friction forces along any surfaces in contact.
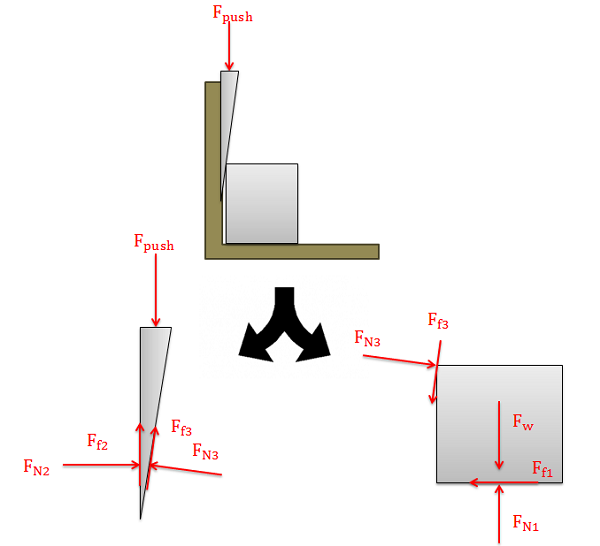
After we draw the free body diagram we can work to simplify the problem. It is usually assumed that the wedge and the bodies will be sliding against one another, so each friction force will be equal to the kinetic coefficient of friction between the two surfaces times the associated normal force between the two forces. This reduces the number of unknowns and will usually allow us to solve for any unknown problems.
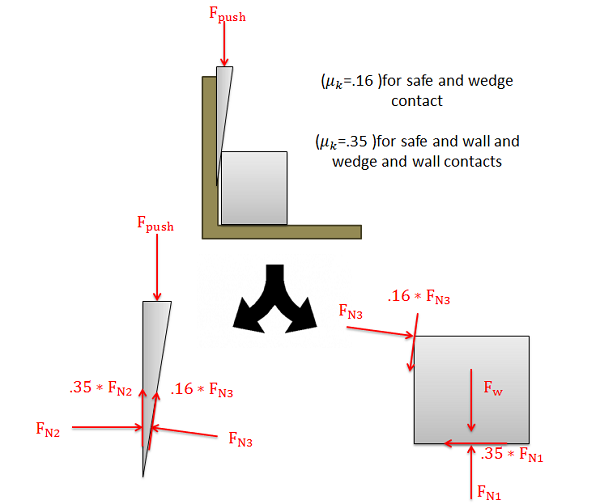
With our simplified diagram we will assume that the bodies are all in equilibrium and we will write our equilibrium equations for the two bodies. By solving the equilibrium equations, we can solve for any unknowns we have.