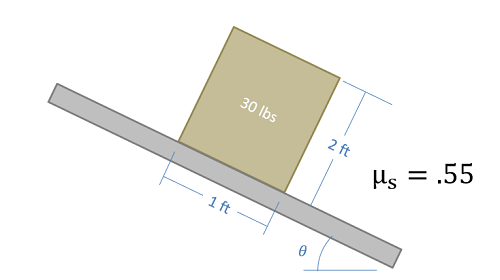
Slipping vs. Tipping
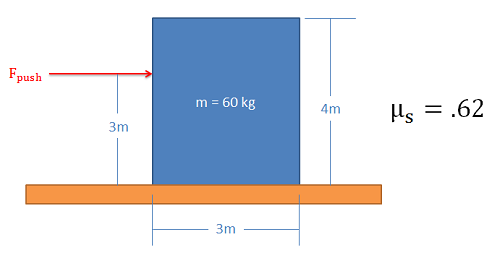
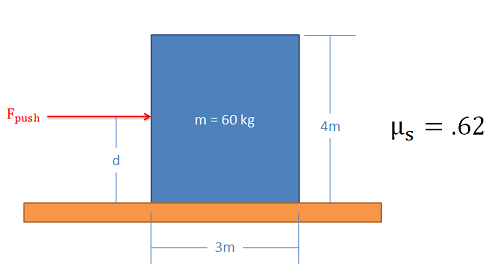
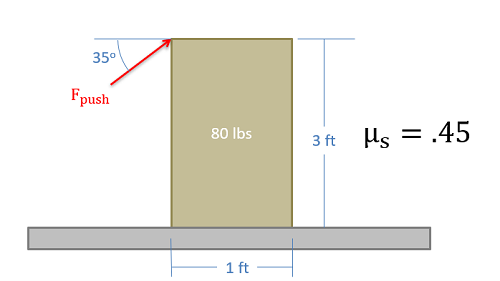
Imagine a box sitting on a rough surface as shown in the figure below. Now imagine that we start pushing on the side of the box. Initially the friction force will resist the pushing force and box will sit still. As we increase the force pushing the box however, one of two things will occur.
- The pushing force will exceed the maximum static friction force and the box will begin to slide across the surface (slipping).
- Or, the pushing force and the friction force will create a strong enough couple that the box will rotate and fall on it's side (tipping).
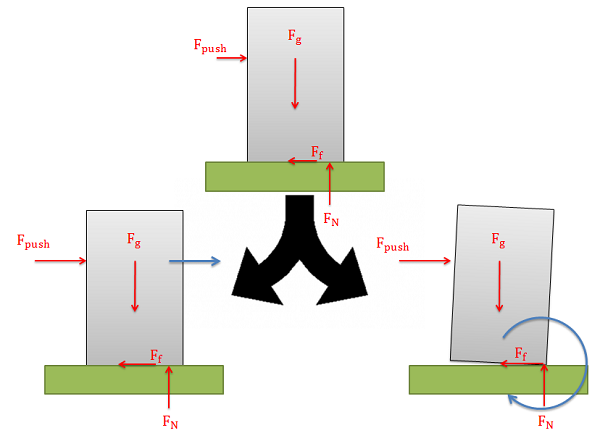
When we look at cases where either slipping or tipping may occur, we are usually interested in finding which of the two options will occur first. To determine this, we usually determine both the pushing force necessary to make the body slide and the pushing force necessary to make the body tip over. Whichever option requires less force is the option that will occur first.
Determining the Force Required to Make an Object "Slip":
A body will slide across a surface if the pushing force exceeds the maximum static friction force that can exist between the two surfaces in contact. As in all dry friction problems, this limit to the friction force is equal to the static coefficient of friction times the normal force between the body. If the pushing force exceeds this value then the body will slip.
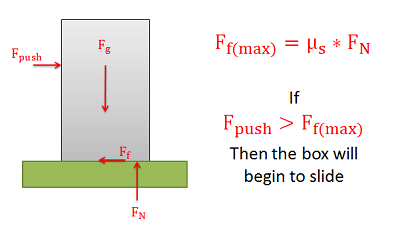
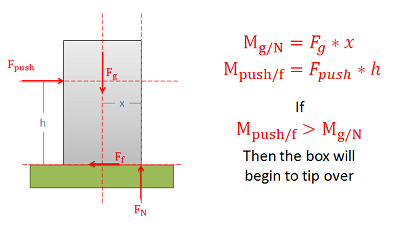
Determining the Force Required to Make an Object "Tip"
The normal forces supporting bodies are distributed forces. These forces will not only prevent the body from accelerating into the ground due to gravitational forces, but they can also redistribute themselves to prevent a body from rotating when forces cause a moment to act on the body. This redistribution will result in the equivalent point load for the normal force shifting to one side or the other. A body will tip over when the normal force can no longer redistribute itself any further to resist the moment exerted by other forces (such as the pushing force and the friction force).
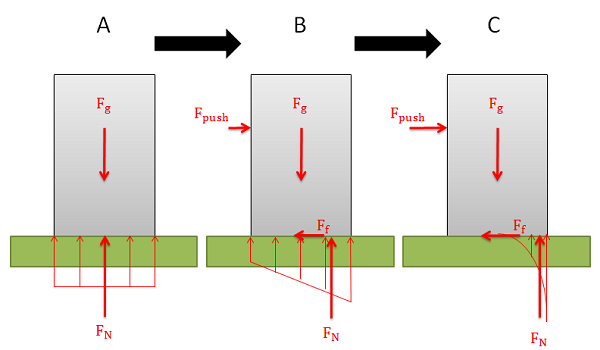
The easiest way to think about the shifting normal force and tipping is to imagine the equivalent point load of the distributed normal force. As we push or pull on the body, the normal force will shift to the left or right. This normal force and the gravitational force create a couple that exerts a moment. This moment will be countering the moment exerted by the couple formed by the pushing force and the friction force.
Because the normal force is the direct result of physical contact, we cannot shift the normal force beyond the surfaces in contact (aka. the edge of the box). If countering the moment exerted by the pushing force and the friction force requires shifting the normal force beyond the edge of the box, then the normal force and the gravity force will not be able to counter the moment and as a result the box will begin to rotate (aka. tip over).