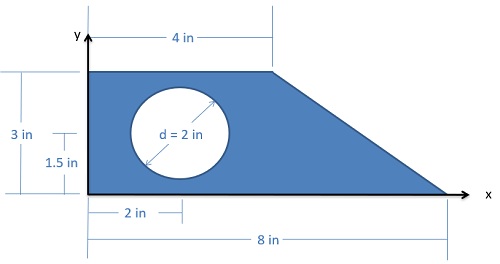
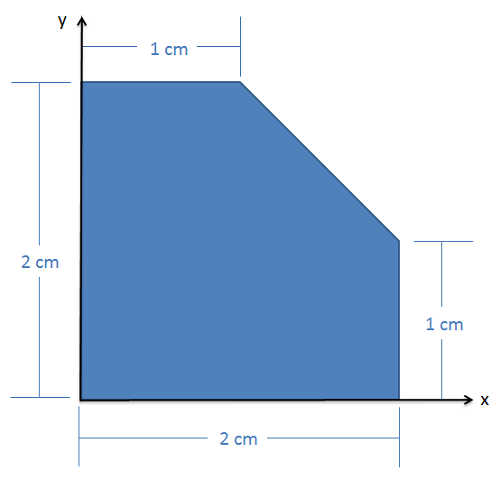
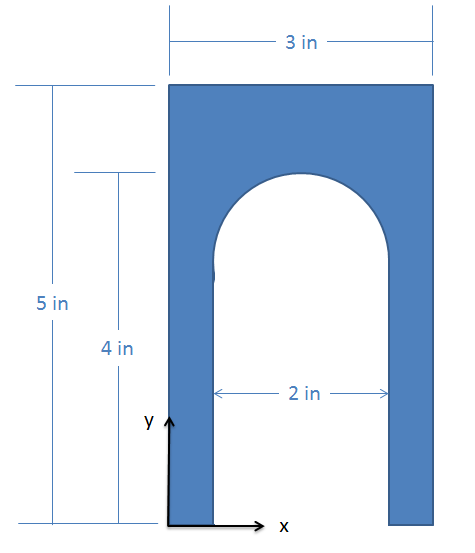
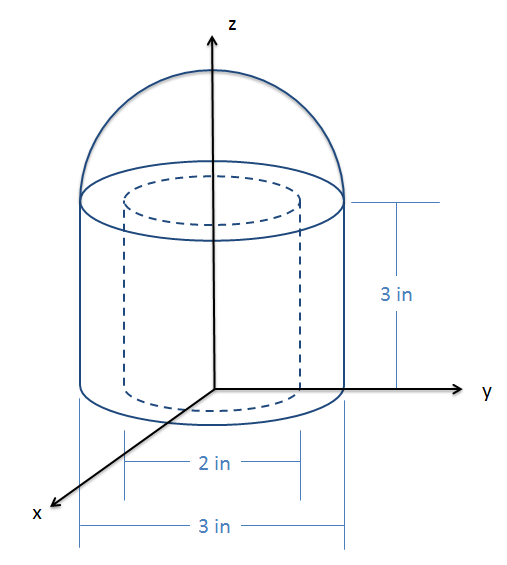
Finding the Centroid and Center of Mass via the Method of Composite Parts
As an alternative to the use of moment integrals, we can use the Method of Composite Parts to find the centroid of an area or volume or the center of mass of a body. This method is often easier and faster that the integration method; however, it will be limited by the table of centroids you have available. The method works by breaking the shape or volume down into a number of more basic shapes, identifying the centroids or centers of masses of each part via a table of values, and then combing the results to find the overall centroid or center of mass.
A key aspect of the method is the use of these centroid tables. This is a set of tables that lists the centroids (and usually also moments of inertia) for a number of common areas and/or volumes. Links to some centroid tables can be found in the sidebar to the right. The method of composite parts is limited in that we will need to be able to break our complex shape down entirely into shapes found in the centroid table we have available or the method will not work without also doing some moment integrals.
Finding the Centroid via the Method of Composite Parts
Start the process by labeling an origin point and axes on your shape. It will be important to measure all locations from the same point. Next, we must break our complex shape down into several simpler shapes. This may include areas or volumes (which we will count as positive areas or volumes) or holes (which we will count as negative areas or volumes). Each of these shapes will have a centroid (C) or center of mass (G) listed on the diagram.
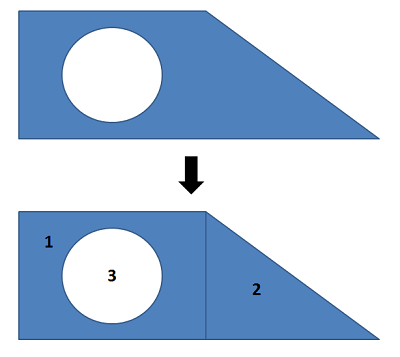
Once we have identified the different parts, we will create a table listing the area or volume of each piece, and the x and y centroid coordinates (or x, y, and z coordinates in 3D). It is important to remember that each coordinate you list should be relative to the same base origin point that you drew in earlier. You may need to mentally adjust diagrams in the centroid tables so that the shape is oriented in the right direction, and account for the placement of the shape relative to the axes in your diagram.
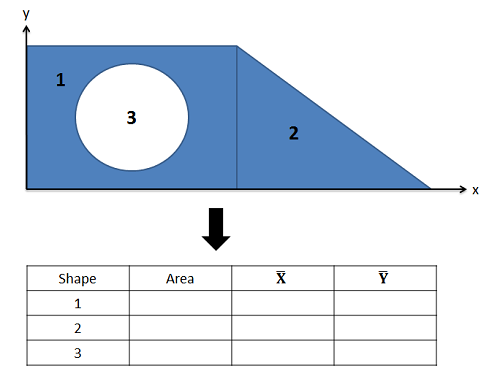
Once you have the areas and centroid coordinates for each shape relative to your origin point, you can find the x and y coordinate of the centroid for the overall shape with the following formulas. Remember that areas or volumes for any shape that is a hole or cutout in the design will be a negative area in your formula.
| \[\bar{x}_{total}=\frac{\sum A_{i}\bar{x}_i}{A_{total}}\] | \[\bar{y}_{total}=\frac{\sum A_{i}\bar{y}_i}{A_{total}}\] |
This generalized formula for the x direction above is simply area one times x̄ one, plus area two times x̄ two, plus area three times x̄ three, adding up as many shapes as you have in this fashion and then dividing by the overall area of your combined shape. The equations are the same for the y location of the overall centroid, except you will instead be using ȳ values in your equations.
For centroids in three dimensions we will simply use volumes in place of areas, and we will have a z coordinate for our centroid as well as the x and y coordinates.
Finding the Center of Mass via the Method of Composite Parts
To use the method of composite parts to find the center of mass, we simply need to adjust the process slightly. First, center of mass calculations will always be in three dimensions. Draw an origin point and some axes on your diagram we did for the centroid. We will measure all locations relative to this origin point. We will then need to break the complex shape down into simple volumes, with each simple volume being something in the centroid table we have available. Remember that when we have a part with a uniform material, the centroid and center of mass are the same point, so we will often talk about these interchangeably.
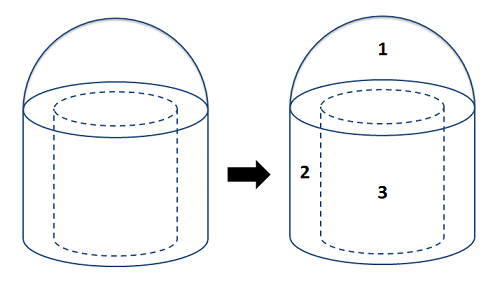
Once we have identified the different parts, we will create a table indicating the mass of each part, and the x, y, and z coordinate of the center of mass for each individual part. It is important to remember that each coordinate you list should be relative to the same base origin point, so you will need to mentally rotate and position the parts in the table relative to your chosen axes.
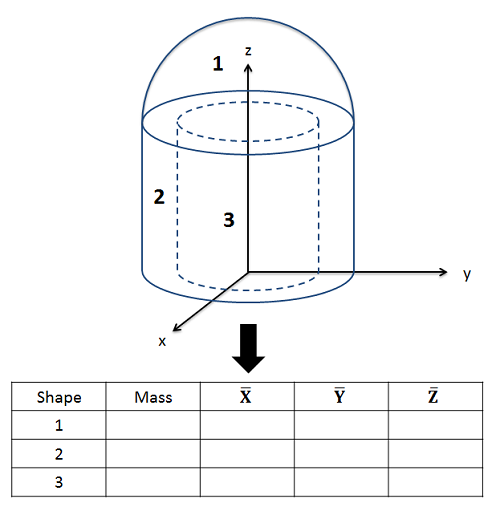
One complicating factor with mass can be measuring the mass of the pieces separately. If we have a scale, we may simply know the overall mass without knowing the mass of the individual pieces. In these cases, you may need work backwards to calculate the density of the material (by dividing overall mass by overall volume) and then use density times piece volume to find the mass of each piece individually. When doing this remember count cutouts as negative mass in your calculations. For example, for the hollow cylinder in the shape above, the "mass" of shape two would be the mass of a solid cylinder (density times volume), and the "mass" of shape three would be the negative of the mass of the cutout cylinder (volume times density).
Finally, once you have the mass the and center of mass coordinates for each shape, you can find the coordinates of the center of mass for the overall volume with the following formulas.
| \[x_{G}=\frac{\sum m_{i}\bar{x}_i}{m_{total}}\] | \[y_{G}=\frac{\sum m_{i}\bar{y}_i}{m_{total}}\] | \[z_{G}=\frac{\sum m_{i}\bar{z}_i}{m_{total}}\] |
Similar to the centroid equations, the x equation is simply mass one times x̄ one, plus mass two time x̄ two, and so on for each part. After you have all the shapes on the top, just divide by the total mass.