Friction (Coloumb) Damped Free Vibration
Friction can also provide vibration damping. In this case, however, the damping is not proportional to the magnitude of velocity. It only depends on the direction of velocity.
We remember from the section on dry friction that the force of friction in sliding depends only on the coefficient of kinetic friction, μk, and the normal force, FN.
| \[F_{f}=\mu_{k}F_{N}\] |
The above equation does not include velocity. We know that kinetic friction acts to oppose motion, however, so a more complete expression would be:
| \[F_{f}=-sgn(\dot{x})\mu_{k}F_{N}\] |
Where sgn is the "sign" function, a function that captures the sign (direction) of velocity. The above equation then indicates that the direction of friction is always opposite the direction of velocity, but the magnitude of velocity does not make a difference in the magnitude of friction.
The equation of motion of the system becomes:
| \[ m \ddot{x} + \mu mg \, \text{sgn}(\dot{x}) + kx = 0 \] |
And the solution to this equation of motion is:
| \[ x(t) = (x_0 - \frac{(2n-1)\mu m g}{k})\cos \omega_n t + \frac{\mu mg}{k}(-1)^{n+1} \] |
where n is the number of half cycles of oscillation completed by the system.
If we plot the response, we can see that there are several differences from a system with viscous damping.
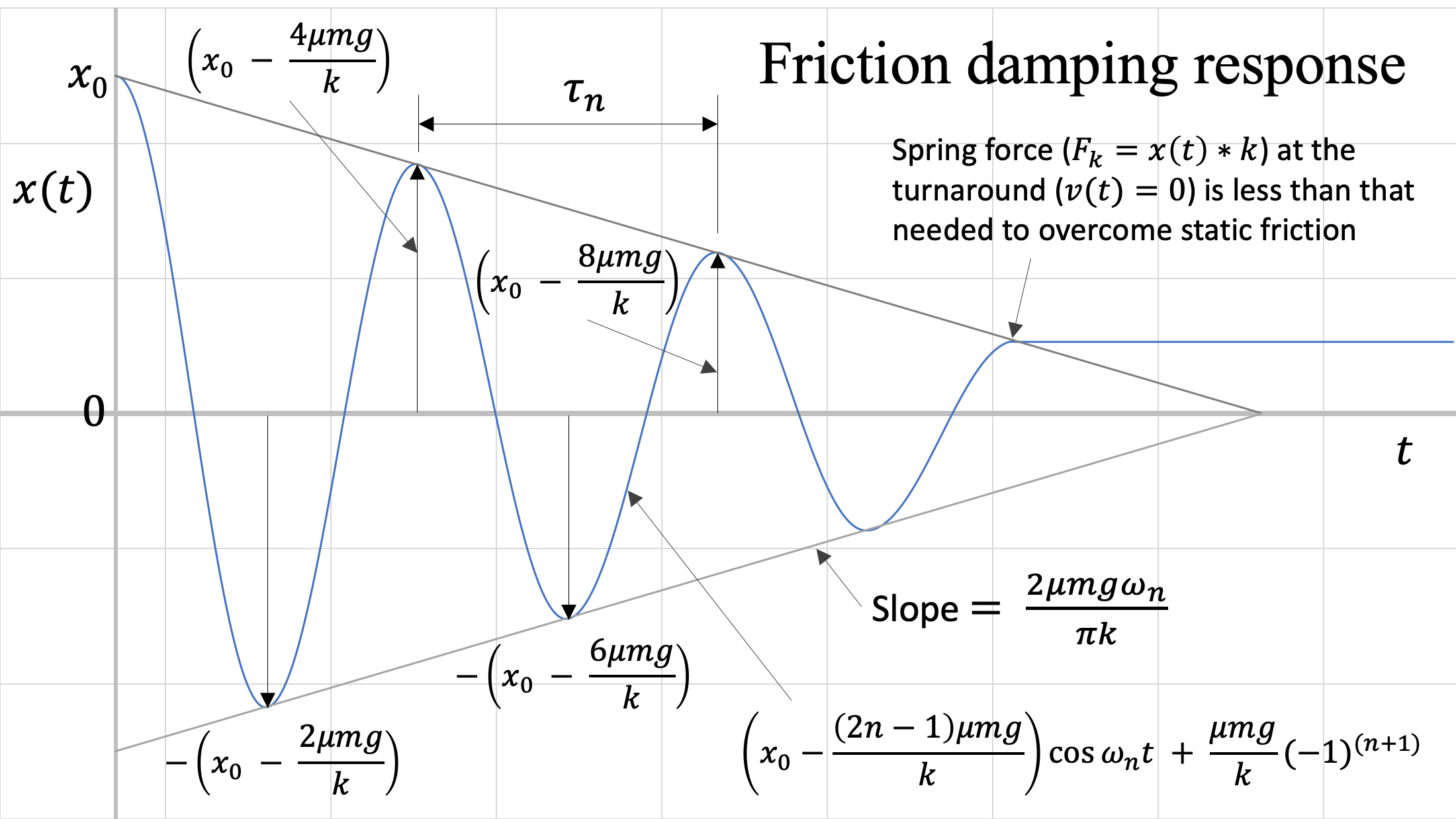
Some differences when compared to viscous damping include:
- The system oscillates at the natural frequency of the system, not a damped natural frequency.
- The bounding curves are linear, not exponential.
- The system does not return to zero. This is because the magnitude of the friction force does not diminish as the system amplitude reduces, and at some point the spring force is no longer able to overcome the static friction that the system experiences when it changes direction (v = 0).
Comparison to Viscous Underdamped System
If we consider our simple linear mass-spring system, the magnitude of Ff does not change with velocity, unlike with viscous damping. If we plotted both types of damping for the same system, we would get the following:
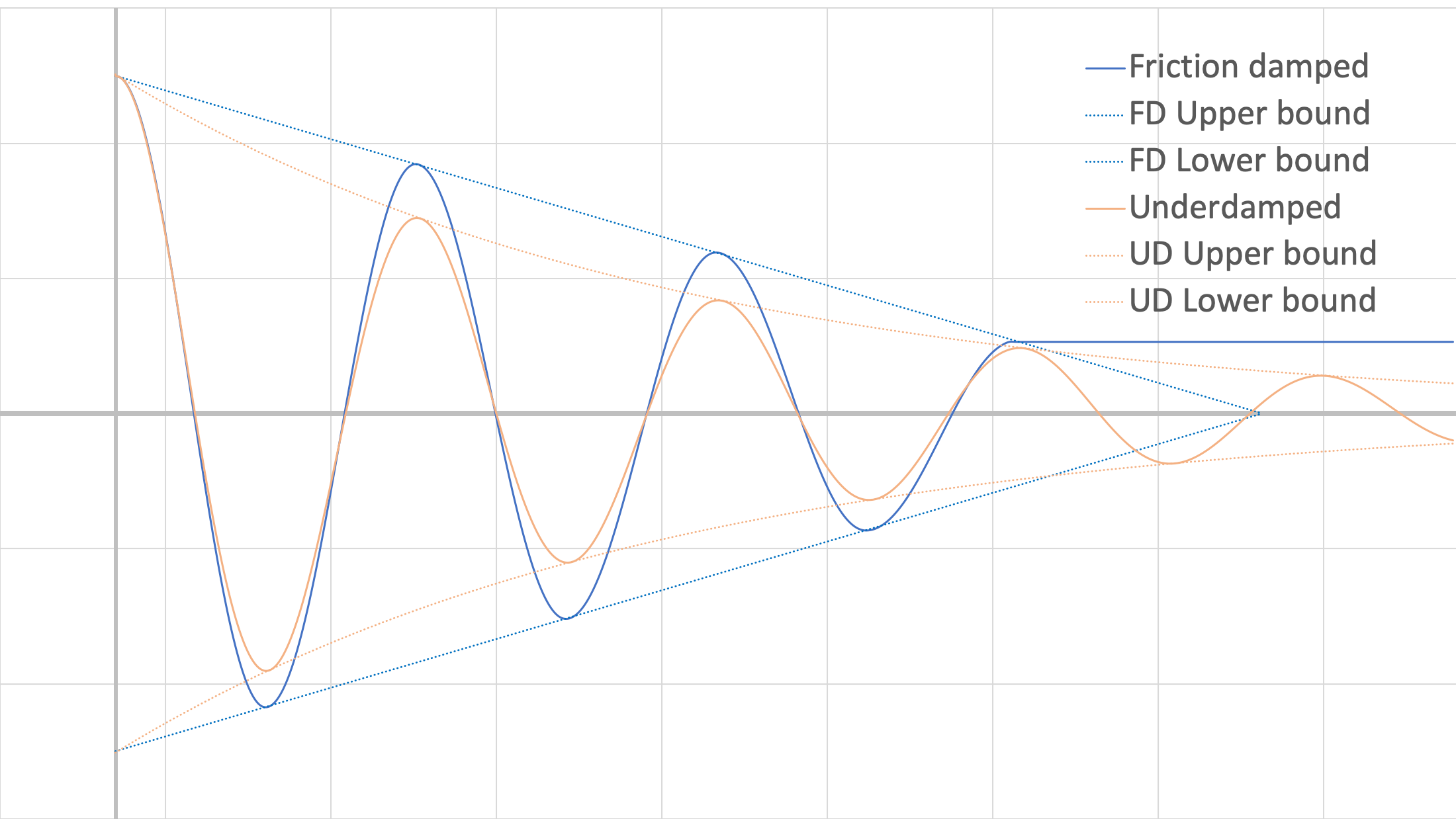
Note that the viscous damping has more reduction in amplitude earlier (despite relatively light damping), but continues oscillating past the point when the friction-damped system has stopped (specific relative values are dependant on the values of damping constant and coefficients of friction). Also note that since the viscous damping is relatively light, the difference in period between the two plots is quite small in this example.