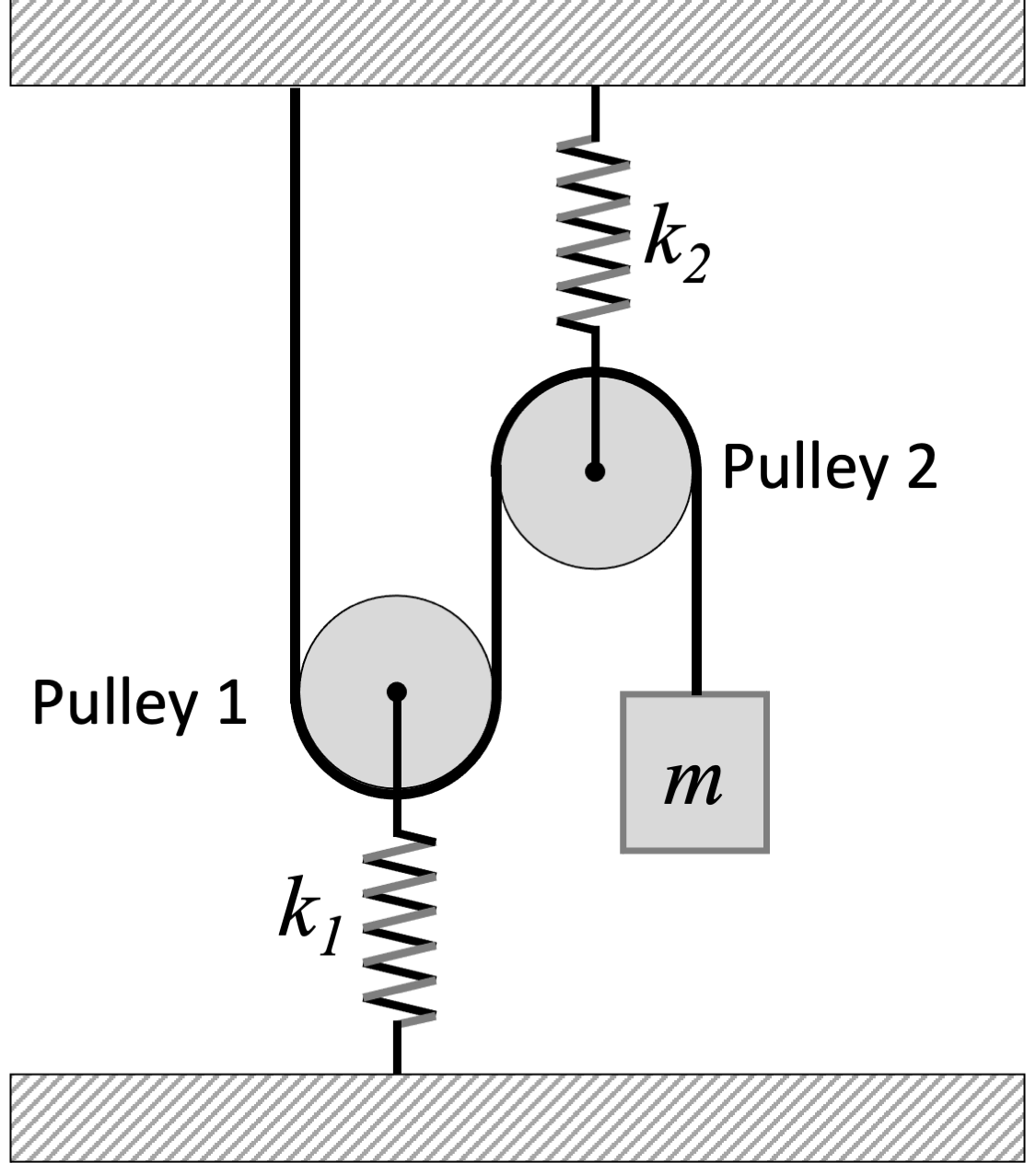
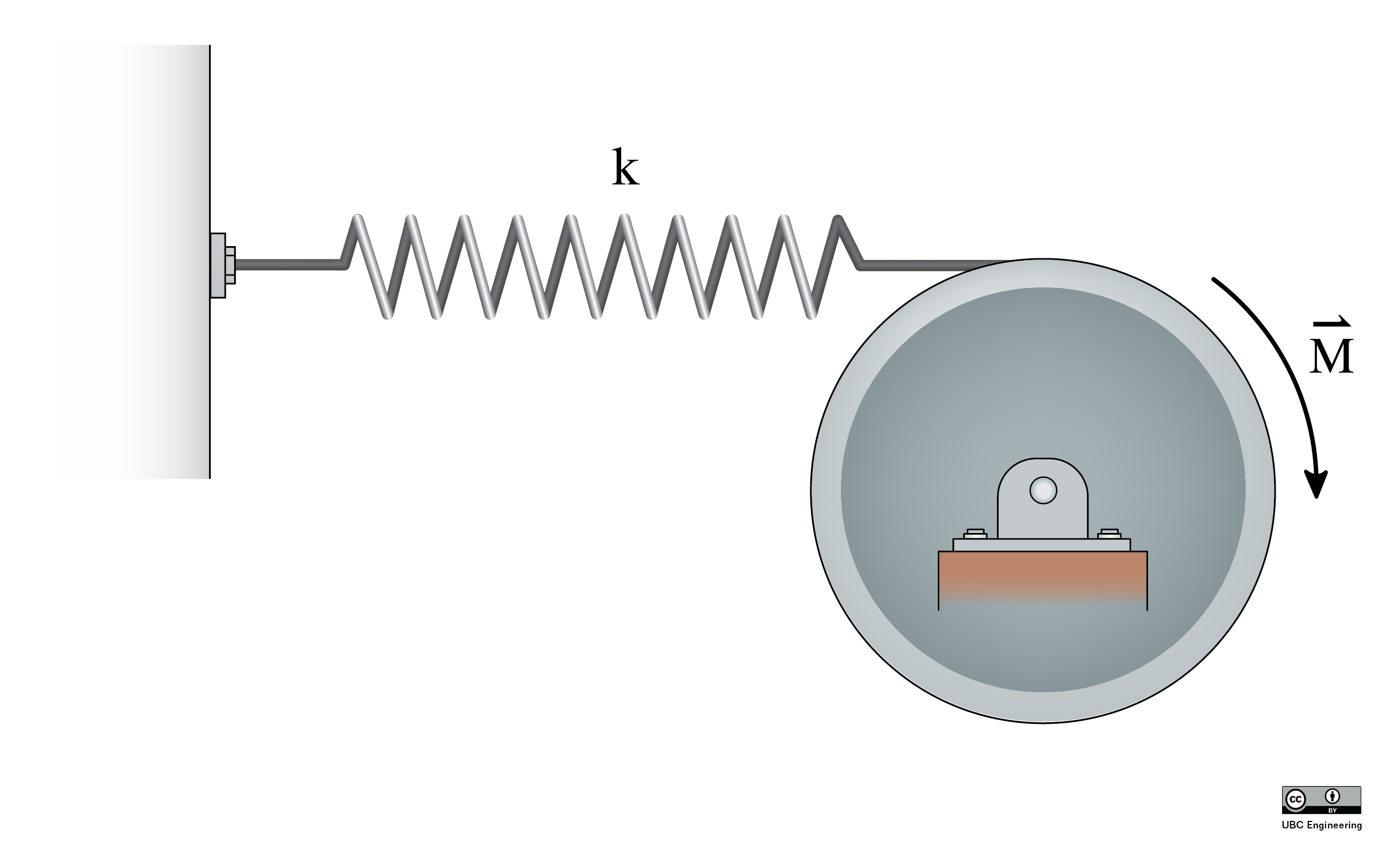
Undamped Free Vibrations
Vibrations occur in systems that attempt to return to their resting or equilibrium state when perturbed (or pushed away from their equilibrium state). The simplest vibrations to analyze are undamped, free, one degree of freedom vibrations.
"Undamped" means that there are no energy losses with movement (whether intentional, by adding dampers, or unintentional, through drag or friction). An undamped system will vibrate forever without any additional applied forces. A simple pendulum has very low damping, and will swing for a long time before stopping. ("Damped" means that there are resistive forces and energy losses with movement that cause the system to stop moving eventually.)
"Free" means that, after the initial perturbation, the only forces acting on the system are internal to the system (springs, dampers) and/or gravity. A tuning fork continues to vibrate after one initial perturbation (being struck). ("Forced" means there is an external, typically periodic, force acting on the system. A jackhammer vibrates due to having a supply of compressed air continually forcing the bit up and down, and it stops vibrating very quickly without that external periodic forcing).
"One degree of freedom" means that we will only consider systems with one mass vibrating along one direction (e.g. use variable x) or about one axis (e.g. use variable θ). Systems having more than one mass or vibrating along or about two or more axes have more than one degree of freedom.
We can derive the equation of the system by setting up a free-body diagram. Consider a mass sitting on a frictionless surface, attached to a wall via a spring.
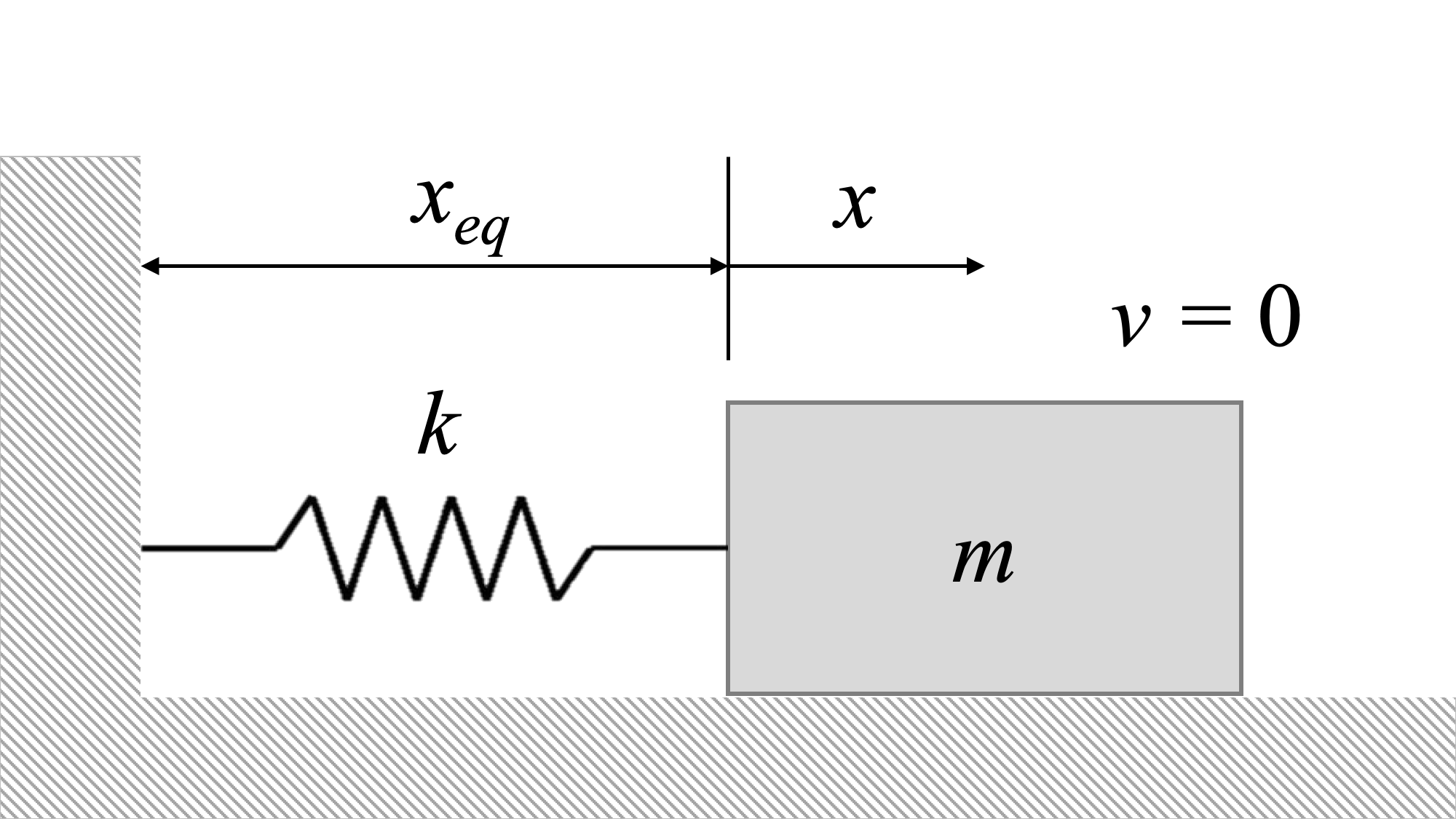
The system above is in equilibrium. It is at rest, and will stay at rest unless some other force acts on it.
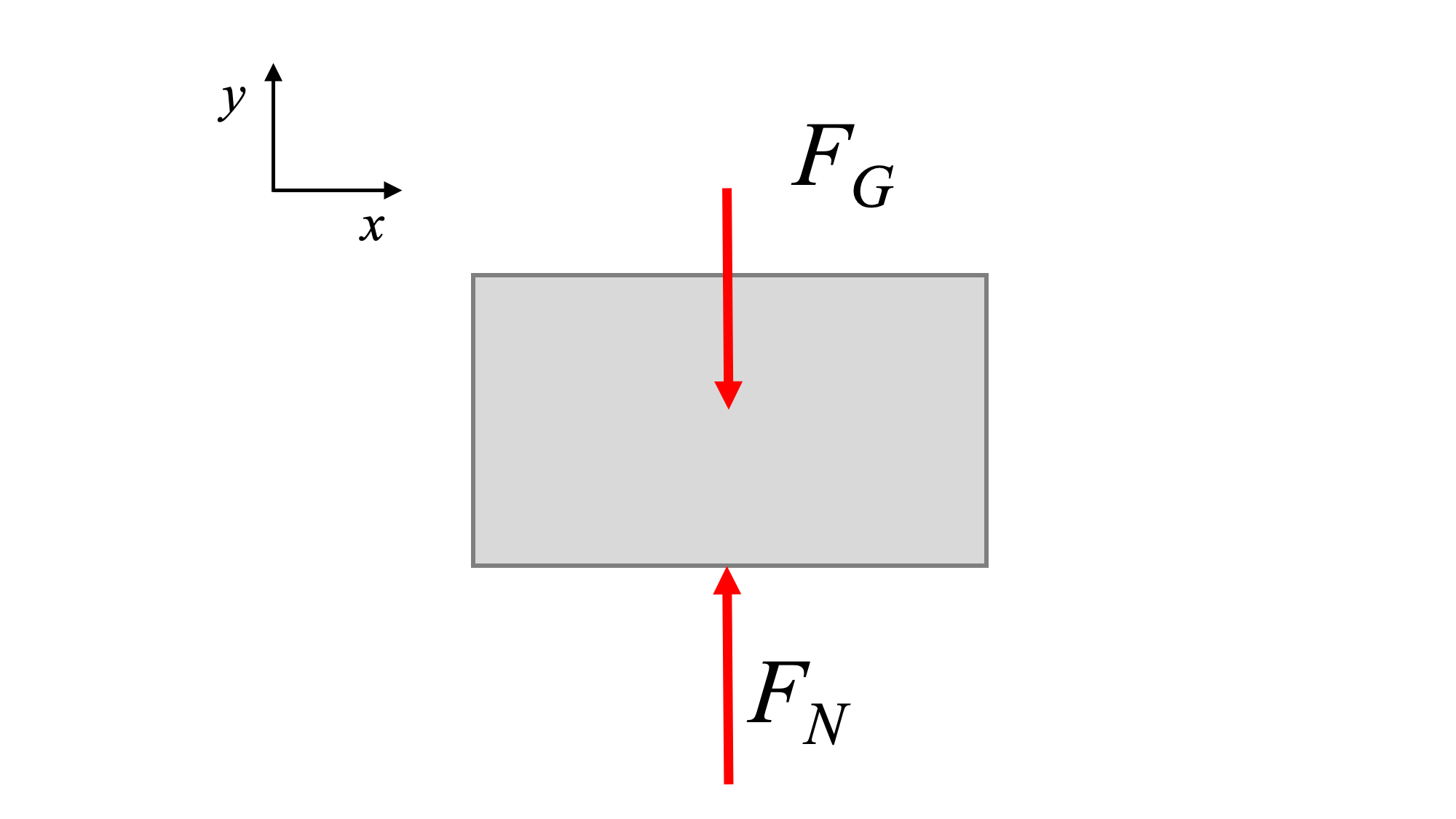
To start the system vibrating, we need to perturb it. Perturbation is moving the system away from equilibrium by a small amount.
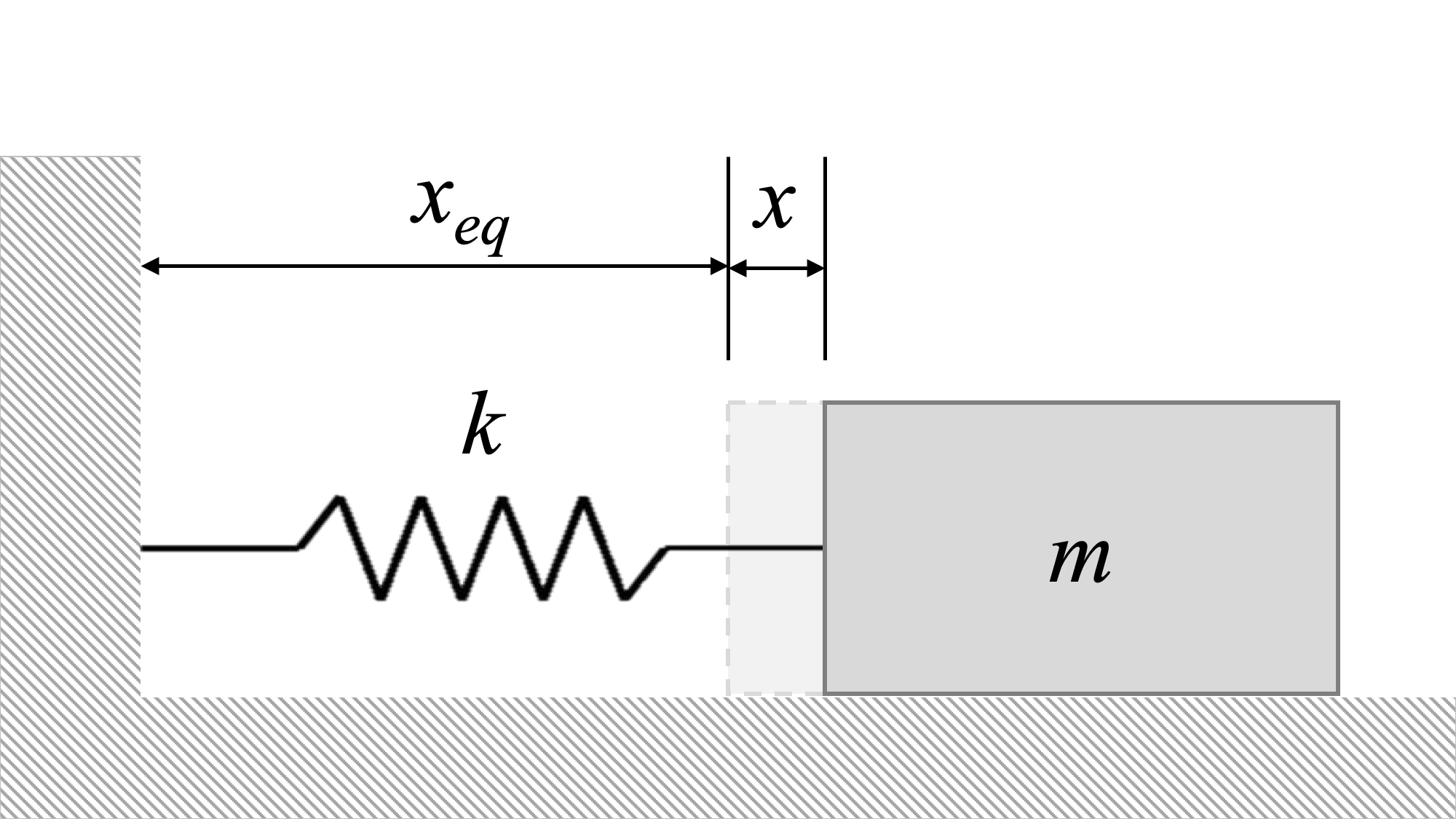
When we perturb this system, we stretch the spring. This generates a spring force, and the spring force is always in a direction that tends to pull the system back toward equilibrium.
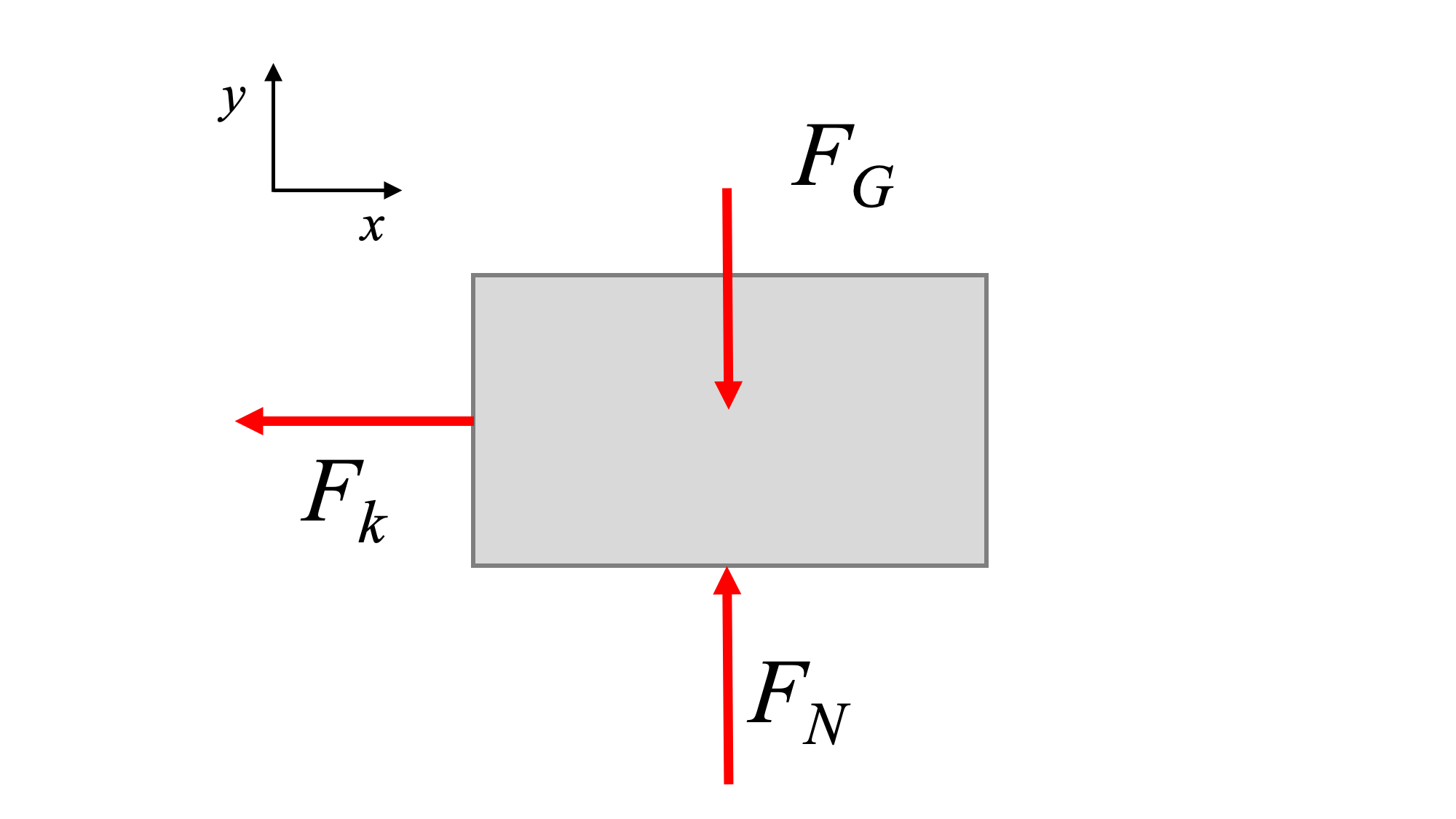
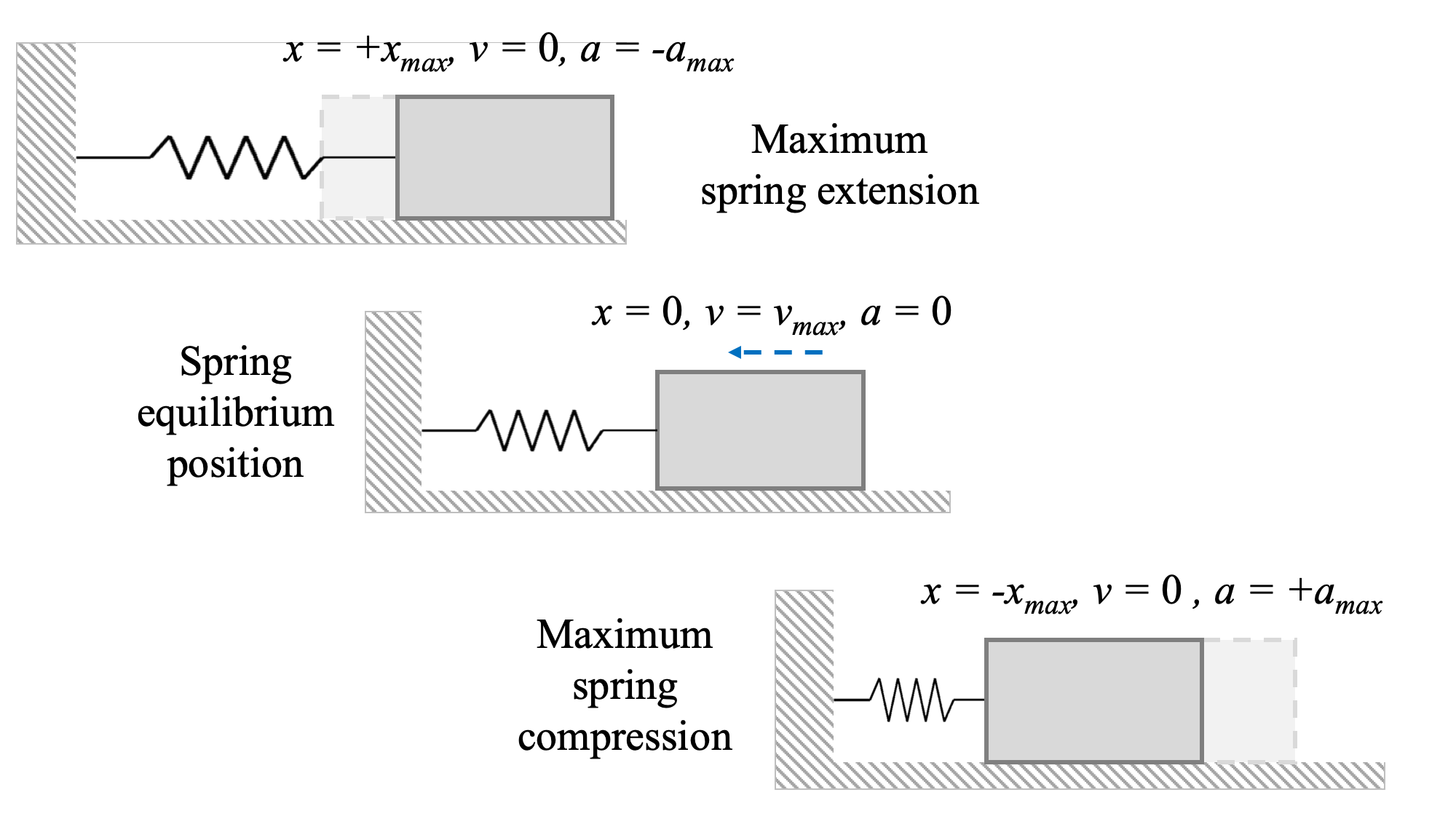
We can generate the equation of motion of the system, and determine the specifics of how it will vibrate, by analyzing this perturbed state. Recall that the spring force or moment is:
| \[\vec{F{_k}} =k \vec{x} \] |
| \[\vec {M{_k}}=k \vec{θ} \] |
Note that the spring constants in the above equations have different units, depending on whether the spring is linear (N/m) or torsional (N-m/rad), and that θ must be given in radians. The magnitude of the spring force depends on x, the distance from the spring unstretched length (not necessarily the equilibrium position of the system), and the same is true for moment of a torsional spring. The spring force or moment is in the direction/orientation opposite that of the displacement. That is, if you pull the mass to the right, the spring force points to the left.
The process for finding the equation of motion of the system is as follows:
- Sketch the system with a small positive perturbation (x or θ).
- Draw the free-body diagram of the perturbed system. Ensure that the spring force has a direction opposing the perturbation.
- Find the one equation of motion for the system in the perturbed coordinate using Newton's Second Law. Keep the same positive direction for position, and assign positive acceleration in the same direction.
- Move all terms of the equation to one side, and check that all terms are positive. If all terms are not positive, there is an error in the direction of displacement, acceleration, and/or spring force.
For the example system above, with mass m and spring constant k, we derive the following:
| \[ \sum F_x = m a_x = m {\ddot{x}} \] |
| \[ -F_k = m {\ddot{x}} \] |
| \[ -k x = m {\ddot{x}} \] |
| \[ m {\ddot{x}} + k x = 0 \] |
This gives us a differential equation that describes the motion of the system. We can rewrite it in normal form:
| \[ m {\ddot{x}} + k {x} = 0 \] |
| \[ \Rightarrow \, {\ddot{x}} + \frac{k}{m} {x} = 0 \] |
| \[ \Rightarrow \, {\ddot{x}} + \omega_n^2 {x} = 0 \] |
The term ωn is called the angular natural frequency of the system, and has units of rads/s.
| \[ \omega_n^2 = \frac{k}{m} \] |
| \[ \omega_n = \sqrt{\frac{k}{m}} \] |
Assuming that the initial perturbation of the system can be described by the position and velocity of the mass at t=0,
| \[ x(0) = x_0 \] |
| \[ v(0) = \dot{x}(0) = v_0 \] |
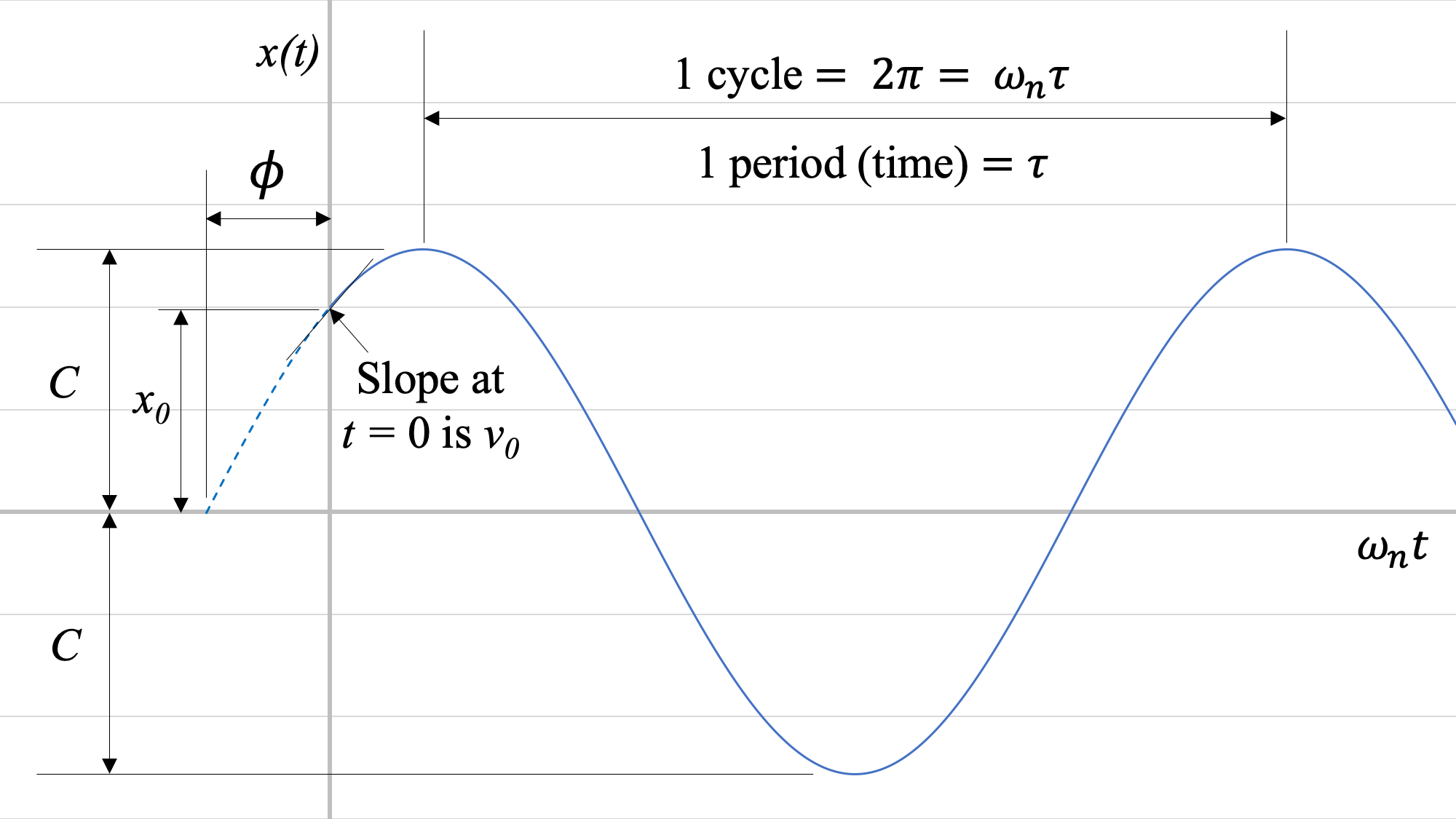
The solution to the differential equation, that provides the position of the system at time t, x(t) is:
| \[ x(t) = C \sin (\omega_n t + \phi) \] |
| \[ \text{where:} \,\, \omega_n = \sqrt{\frac{k}{m}}, \, C = \sqrt{(\frac{v_0}{\omega_n})^2 + x_0^2}, \, \phi = \tan^{-1} (\frac{x_0 \omega_n}{v_0}) \] |
The amplitude, C, describes the maximum displacement during the oscillations (i.e. xmax) and the phase, ϕ, describes how the sine function is shifted in time.
For a system where there is torsional vibration (that is, the oscillation involves a rotation), the equations are similarly:
| \[ I {\ddot{\theta}} + k{\theta} = 0 \] |
| \[ \Rightarrow \, {\ddot{\theta}} + \frac{k}{I}{\theta} = 0 \] |
| \[ \Rightarrow \, {\ddot{\theta}} + \omega_n^2 {\theta} = 0 \] |
| \[ \text{where:} \,\, \omega_n = \sqrt{\frac{k}{I}} \] |
Assuming that the initial perturbation of the system can be described by the position and velocity of the mass at t=0,
| \[ \theta (0) = \theta_0 \] |
| \[ \omega (0) = \dot{\theta} (0) = \omega_0 \] |
The solution to the differential equation, that provides the position of the system at time t, θ(t) is:
| \[ \theta (t) = C \sin (\omega_n t + \phi) \] |
| \[ \text{where:} \,\, \omega_n = \sqrt{\frac{k}{I}}, \, C = \sqrt{(\frac{\omega_0}{\omega_n})^2 + \theta_0^2}, \, \phi = \tan^{-1} (\frac{\theta_0 \omega_n}{\omega_0}) \] |