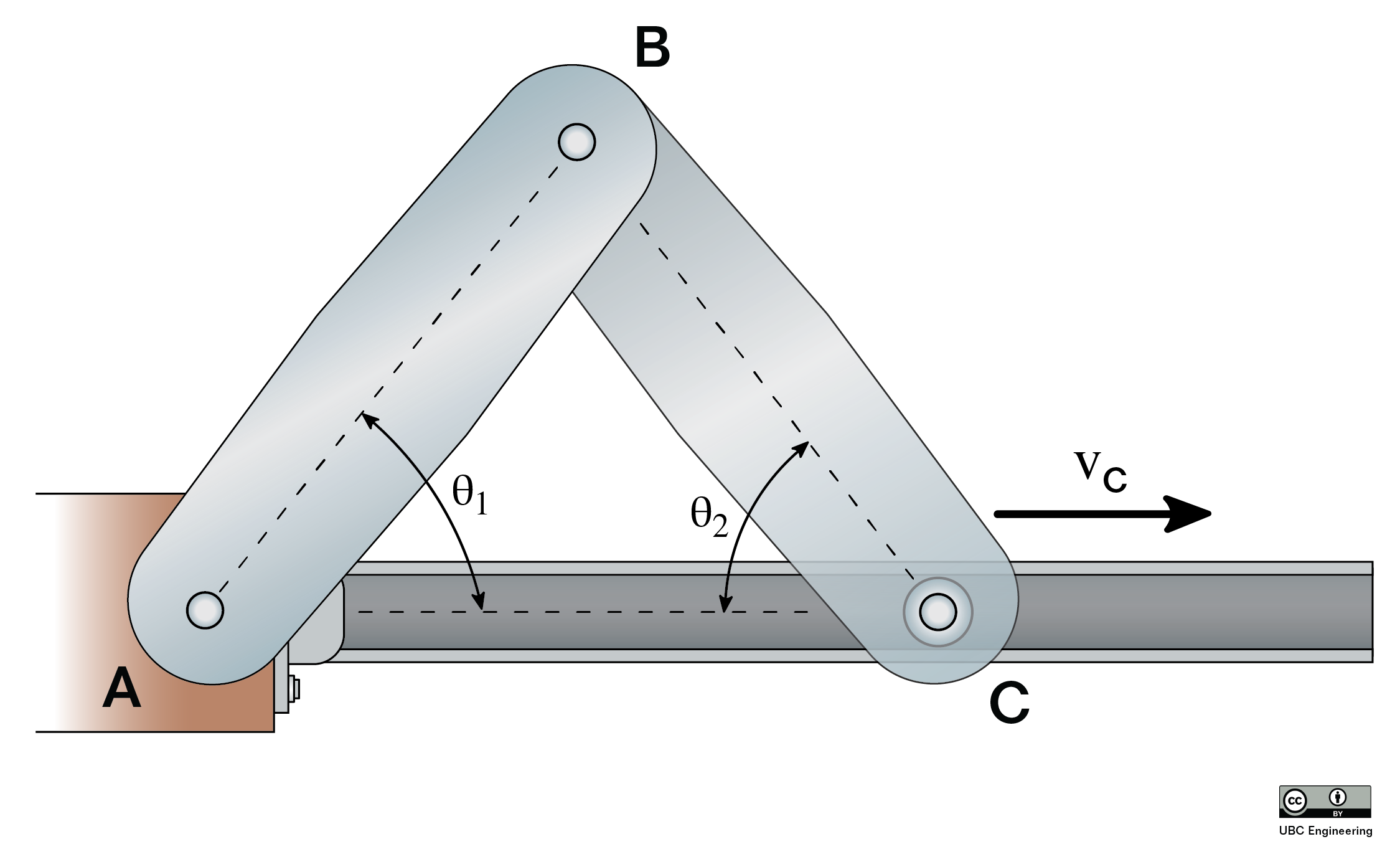
Absolute Motion Analysis
Absolute motion analysis is one method used to analyze bodies undergoing general planar motion. General planar motion is motion where bodies can both translate and rotate at the same time. Besides absolute motion analysis, the alternative is relative motion analysis. Either method can be used for any general planar motion problem, however one method may be significantly easier to apply in certain situations.
Absolute motion analysis will require calculus and is generally faster for simple problems and problems where only the velocities (and not accelerations) are required. Relative motion analysis will not require calculus, but does necessitate using multiple coordinate systems and is generally easier to use for more complex problems and problems where velocities and accelerations are being analyzed.
Utilizing Absolute Motion Analysis
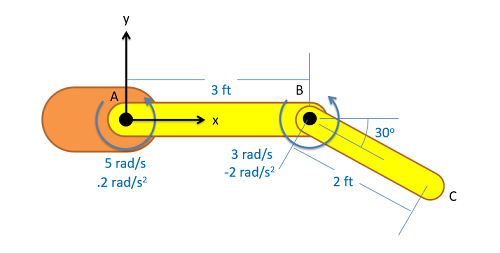
To start our discussion on absolute motion analysis, we are going to imagine a simple robotic arm such as the one below. In this arm, we have two arm sections of fixed length with motors causing rotations at joint A and joint B.
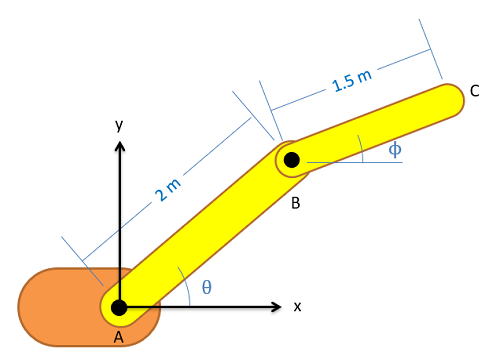
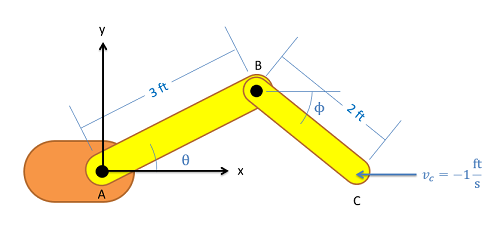
The first step in absolute motion analysis is come up with a set of equations describing the position of some point of interest. In this case we will be looking at the position of the end effector of the arm at point C, and we will write an equation for the x position and the y position of this point with respect to the fixed origin point at A. In these equations, anything that is a constant (such as the length of the arm pieces) can be put in as a number, but anything that will change (such as angles theta and phi) will need to remain as variables in these equations even if they are known at the moment. Using the values in the diagram we would wind up with the two following position equations.
| X Position: | \[x_{c}=2cos(\theta)+1.5cos(\phi)\] |
|---|---|
| Y Position: | \[y_{c}=2sin(\theta)+1.5sin(\phi)\] |
To find the velocity of point C in the x and y directions, we simply need to take the derivatives of the position equations. The velocity equations for our robotic arm are below.
| X Velocity: | \[v_{xc}=-2sin(\theta)\dot{\theta}-1.5sin(\phi)\dot{\phi}\] |
|---|---|
| Y Velocity: | \[v_{yc}=2cos(\theta)\dot{\theta}+1.5cos(\phi)\dot{\phi}\] |
To find the acceleration of point C in the x and y directions we simply need to take the derivatives of the velocity equations. The acceleration equations for our robotic arm in the x and y directions are shown below.
| X Acc: | \[a_{xc}=-2cos(\theta)\dot{\theta}^{2}-2sin(\theta)\ddot{\theta}-1.5cos(\phi)\dot{\phi}^{2}-1.5sin(\phi)\ddot{\phi}\] |
|---|---|
| Y Acc: | \[a_{yc}=-2sin(\theta)\dot{\theta}^{2}+2cos(\theta)\ddot{\theta}-1.5sin(\phi)\dot{\phi}^{2}+1.5cos(\phi)\ddot{\phi}\] |
Once we have the velocity and acceleration equations, we can start solving for any unknowns. If we have known angular velocities and accelerations (theta dot, theta double dot, phi dot, and phi double dot) we can plug those in to find the velocity and acceleration vectors for the end effector. In other instances, we may known or desired motion of the end effector (vcx, vcy, acx, and acy) and will have to plug those in to the equations to solve for unknowns such as theta dot and so on.