Rigid Body Translation
With rigid bodies, we have to examine moments and at least the possibility of rotation along with the forces and accelerations we examined with particles. Some rigid bodies will translate but not rotate (translational systems), some will rotate but not translate (fixed axis rotation) and some will rotate and translate (general planar motion). Overall we will start with an examination of translational systems, then examine fixed axis rotation, then pull everything together for general planar motion.
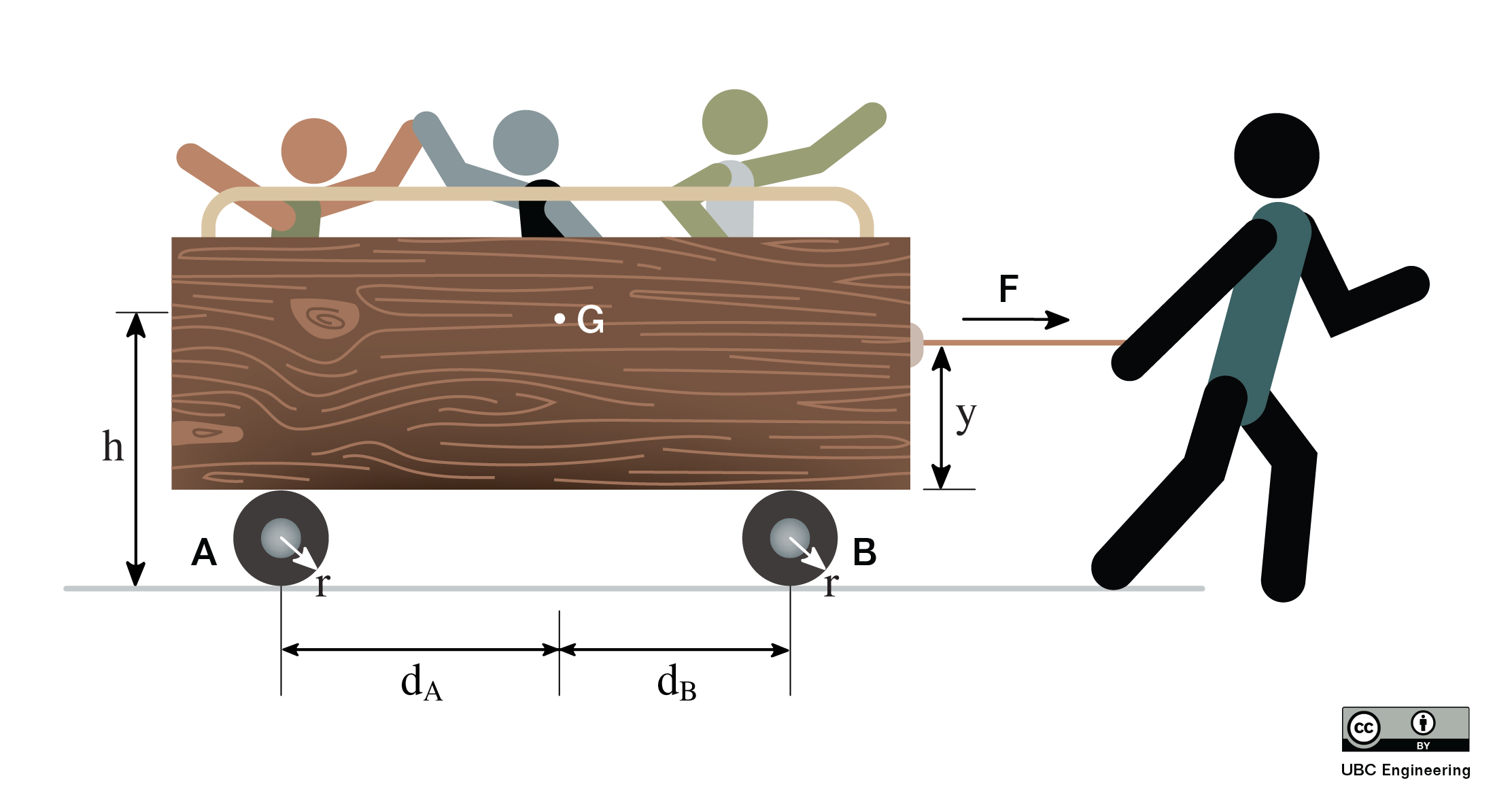
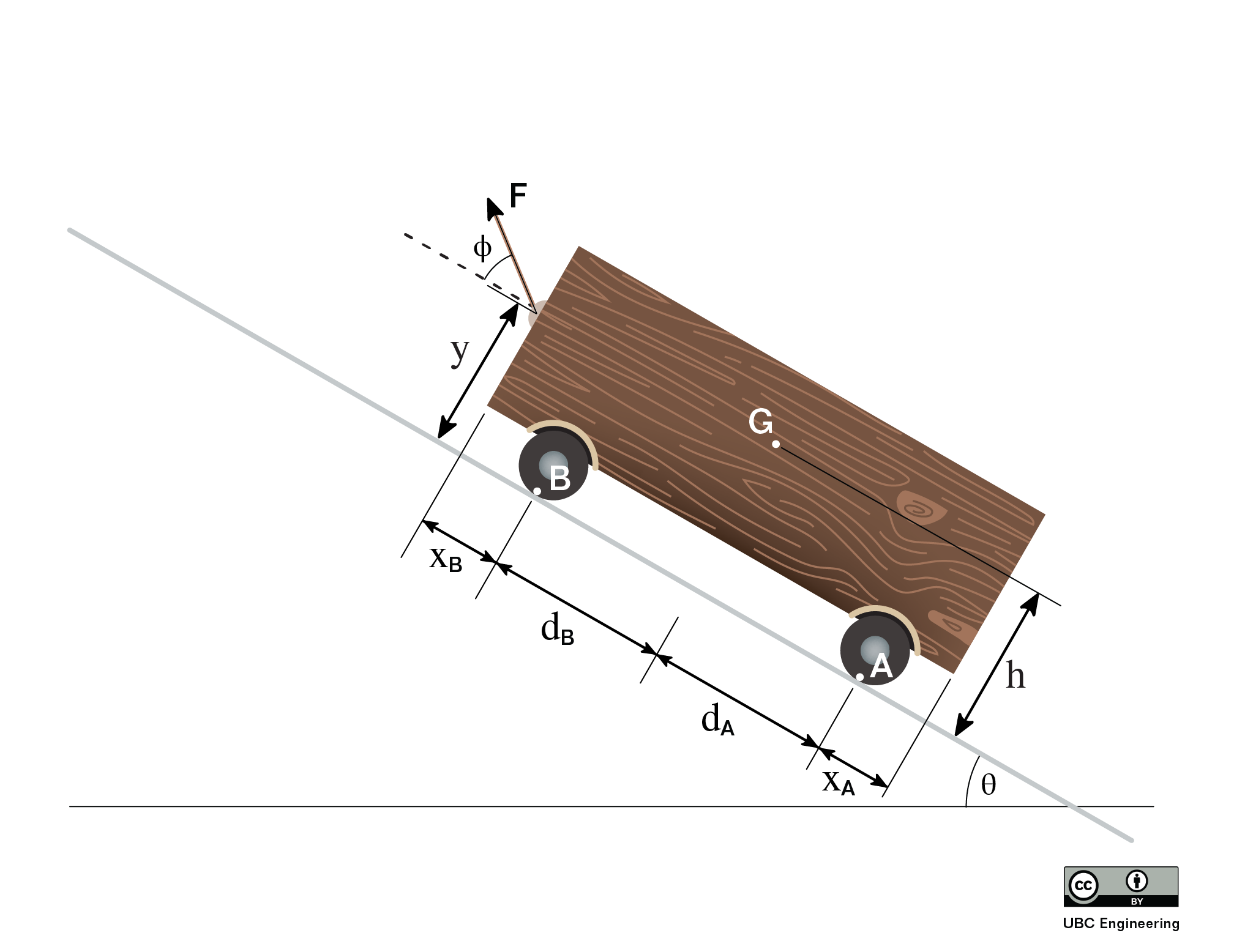
As the start of our analysis, we will go back to Newton's Second Law. Since this is a rigid body system, we include both the translational and rotational versions. Note that now we have bodies with extent, the location of the acceleration and the axis about which we take moments or calculate mass moment of inertia are important. Linear accelerations are always measured at the center of mass. We will develop several moment equations, depending on the point about which moments are taken.
| \[\sum \vec{F}=m*\vec{a_G}\] |
| \[\sum \vec{M_G}=I_G*\vec{\alpha}\] |
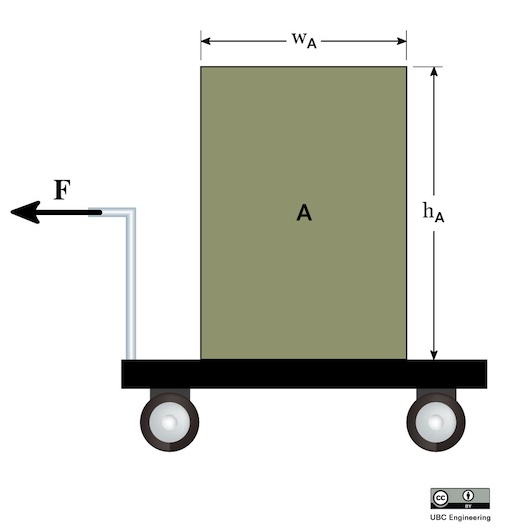
As we did with particles, we can break the vector force equation into components, turning the one vector equation into two scalar equations (in the x and y directions respectively). As for the moment equation, a translational system by definition will have zero angular acceleration. With the angular acceleration being zero, the sum of the moments must all be equal to zero. This is similar to statics problems, however there is one big difference we must take into account. The moments must be taken about the center of mass of the body. Setting the moments to zero about other points will lead to invalid solutions for any body experiencing an acceleration. Putting these specifics into action, we wind up with the three base equations of motion below. To solve for unknown forces or accelerations, we simply draw a free body diagram, put the knowns and unknowns into these equations, and solve for the unknowns.
| \[\sum F_{x}=m*a_{Gx}\] |
| \[\sum F_{y}=m*a_{Gy}\] |
| \[\sum M_{G}=0\] |